حل كتاب الرياضيات للصف السادس ابتدائي الفصل الثاني للعام الدراسي 1446، كتاب الرياضيات متوفر على موقع حلول متضمناً حلول جميع النشاطات والتمارين، كتاب الرياضيات بحسب المناهج الجديدة للمملكة العربية السعودية
حل كتاب الرياضيات سادس ابتدائي
حل الفصل الرابع الكسور الاعتيادية والكسور العشرية
حل الفصل الخامس القياس الطول والكتلة والسعة
فصل العمليات على الكسور الاعتيادية
خمن: قارن بين بسط كل كسر و مقامه في كل مجموعة، ثم بين كيف تقرب أي كسر إلى أقرب نصف دون استعمال نموذج
إذا كان البسط قريبا بصورة كبيرة من المقام فيقرب الكسر إلى الواحد
إذا كان البسط قريبا من نصف المقام فيقرب الكسر إلى نصف
إذا كان البسط أصغر بصورة كبيرة من المقام فيقرب الكسر إلى الصفر
اكتب: اكتب قاعدة لتقريب الكسور إلى أقرب نصف سنتمتر
التقريب إلى نصف: إذا كان البسط قريباً من نصف المقام فقرب الكسر إلي نصف
اكتب: كيف تحدد أن ناتج تقريب كسر ما بالتقريب إلى أقرب نصف هو: صفر أم 1 /2 أم 1؟
إذا كان البسط قريبا بصورة كبيرة من المقام فيقرب الكسر إلي الواحد
إذا كان البسط قريبا من نصف المقام فيقرب الكسر إلي نصف
إذا كان البسط أصغر بصوره كبيره من المقام فيقرب الكسر إلي الصفر
تمرين: اشرح كيف يمكن لهذه الخطة أن تساعد على تحديد معقولية إجابتك بعد الانتهاء من إجراء الحسابات.
بعد تمثيلك المسألة؛ إذا بدت الإجابة معقولة مقارنة بالحسابات يكون احتمال الحل صحيحاً
تمرين: اكتب يمكن حلها باستعمال خطة (تمثيل المسألة) ثم وضح تمثيلها
هي تستطيع الحصول على قطع أطوالها 1.29 م - 0.89 م - 2.99 م من شريط طوله 4.65 م؟
الإجابة: الإجابة: يمكنك أن تحضر شريطاً ورقيا أو بلاستيكياً و مقصاً؛ ثم تمثل الموقف و تجرب الحل
مسألة: يقدم أحد المطاعم وجبة تتكون من الدجاج أو السمك، بالإضافة إلى القهوة أو الشاي أو عصير الليمون أو الماء، فما عدد الطرق الممكنة لوجبة من هذا المطعم؟ اكتب هذه الطرق.
افهم: يقدم أحد المطاعم وجبة تتكون من الدجاج أو السمك بالإضافة إلى قهوة أو الشاي أو عصير الليمون أو الماء فما عدد طرق الممكنة لوجبة من هذا المطعم، المطلوب: اكتب هذه الطرق
خطط: استعمل خطة التمثيل لأجد حل المسألة
حل: الدجاج مع قهوة؛ الدجاج مع شاي؛ الدجاج مع عصير الليمون الدجاج مع الماء؛ السمك مع قهوة؛ السمك مع شاي
السمك مع عصير الليمون، السمك مع الماء، إذن عدد الطرق 8 طرق
تحقق: الإجابة معقولة إذن الإجابة صحيحة
مسألة: اشترك خالد و عمر و فهد و سهيل في سباق جري تتابع، فما عدد التراتيب الممكنة لهذا السباق على أن يكون خالد آخر من يجري؟ ثم اذكرها
افهم: اشترك خالد وعمر وفهد وسهيل في سباق جري تتابع
المطلوب: عدد التراتيب الممكنة لهذا السباق على أن يكون خالد أخر من يجري
خطط: استعمل خطة التمثيل لأجد حل المسألة
حل: عمر و فهد و سهيل و خالد، عمر و سهيل و فهد و خالد
فهد و عمر و سهيل و خالد؛ فهد و سهيل و عمر و خالد
سهيل و عمر و فهد و خالد؛ سهيل و فهد و عمر و خالد
إذن عدد الطرق التي يكون فيها خالد اخر واحد = 6 طرق
تحقق: الإجابة معقولة إذن الإجابة صحيحة
اكتب: قاعدة بسيطة لجمع أو طرح كسرين متشابهين
عند جمع كسرين متشابهين أو طرحهما؛ أجمع البسطين أو أطرحهما وأستعمل المقام المشترك في كتابة الناتج
خمن: ما العلاقة بين عدد أجزاء نموذج كسر الإجابة و مقامي الكسرين المضافين أو المطروحين؟
عدد أجزاء نموذج كسر الإجابة يساوي المضاعف المشترك الأصغر لمقامي الكسور غير المتشابهة
مطويات: اطوِ ورقة من منتصفها، ثم أعد طيها مرة أخرى من منتصفها و كرر ذلك مرتين أخريين، ثم افتح الورقة كاملة، ما عدد الأجزاء الظاهرة في الورقة؟ استعمل خطة تمثيل المسألة
عند طي الورقة للمرة الأولى ينتج جزأين و عند طيها مرة أخرى ينتج 4 أجزاء و عند طيها مرتين أخريين ينتج 16 جزء
تمرين: هل يمكنك أن توزع قطع العد إلى ثلاث مجموعات، بحيث تحتوي كل منها على العدد نفسه من القطع؟ فسر إجابتك
لا يمكن توزيع العدد 16 إلي ثلات مجموعات تحتوي كل منها على العدد نفسه
تمرين: فسر العلاقة بين بسطي الكسرين في المسألة، و بسط الناتج، ماذا تلاحظ حول مقامات الكسرين في المسألة و مقام الناتج؟
بسط الناتج يكون عبارة عن ضرب البسطين و بالمثل يكون مقام الناتج يكون عبارة عن حاصل ضرب المقامين
خمن: اكتب قاعدة تستعملها لضرب الكسور.
ضرب البسوط معا و ضرب المقامات معاً ثم الاختصار إن أمكن
تمرين: ما العلاقة بين بسطي العاملين (الكسرين) و مقامهما مع بسط الناتج و مقامه؟
الناتج عبارة عن حاصل ضرب البسطين معاً و المقامين معاً
فصل النسبة و التناسب
تمرين: تبرع 24 طالباً من الصف الخامس بـــ 144 ريال لمساعدة الطلاب المحتاجين، بينما تبرع 28 طالباً من الصف السادس بــ 196 ريالاً، فأيهما كان معدل تبرعه أكثر، طالب الصف الخامس أم طالب الصف السادس؟ فسر إجابتك.
نسبة تبرعات الصف الخامس = 144 /24 = 6 /1
اقسم البسط و المقام على 24 لمعرفة معدل تبرع الطالب الواحد
نسبة تبرعات الصف السادس = 196 /28 = 7 /1
اقسم البسط و المقام على 24 لمعرفة معدل تبرع الطالب الواحد
إذا معدل تبرع الطالب في الصف السادس أكبر من معدل تبرع الطالب في الصف الخامس
اكتب: ما الفرق بين النسبة و المعدل؟ أعطِ مثالين على كل منهما
النسبة هي عبارة عن المقارنة بين كميتين متشابهتين في الوحدة باستعمال القسمة؛أما المعدل هو نسبة يين كميتين بوحدتين مختلفتين
النسية مثل النسية بين عدد المشابك الحمراء إلى عدد المشابك الزرقاء = 2 : 6
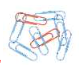
أما المعدل مثل المقارنة بين الريالات السعودية و الدينار الأردني كما بالشكل
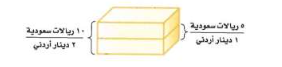
تمرين: أوجد النسبة في أبسط صورة بين مقدار كل من العصير المركز و الماء اللازمين لعمل إبريق من عصير البرتقال المخفف، ثم إبريقين، ثم 3 أباريق، ماذا تلاحظ؟
قارورة واحدة النسبة 1 : 3 في أبسط صورة
قارورتين نقسم البسط و المقام على 2 لنحصل على النسبة 1 : 3 أبسط صورة
3 قوارير نقسم البسط و المقام على 3 لنحصل على النسية 1 : 3
تلاحظ أن جميع النسب متساوية في أبسط صورة
تمرين: تحتاج سيدة إلى أربع كرات من الصوف لصنع 8 قبعات، فكم كرة من الصوف تحتاج لصنع 6 قبعات؟
بما أن ليس هناك عدد صحيح تقسم عليه 8 لينتج 6، إذاً تضرب كل الكميات في 3 ثم تقسم على 4، إذاً تحتاج 3 كرات صوف لعمل 6 قبعات
تمرين: إذا علمت أن 48 جراماً من شراب السكر تكفي لإطعام 8 طيور طنانة في اليوم، و كان لديك 36 جراماً من شراب السكر، فكمطائراً تكفي هذه الكمية؟
بما أن ليس هناك عدد صحيح تقسم عليه 48 لينتج 36 تقسم كل الكميات على 8، ثم تضرب في 6، إذاً 36 شراب السكر يكفي لإطعام 6 طيور.
تمرين: قطع خالد 190 كيلو متراً في 4 أ]ام على دراجة هوائية فإذا أكمل الرحلة بالمعدل نفسه، فكم كيلو متراً يقطع في 6 أيام؟
بما أن لا يوجد عدد صحيح يضرب في 4 ليعطي 6، لذا نقسم على 2 ثم نضرب في 3 إذاً بعد 3 أيام يقطع 285 كيلومتر
تمرين: 16 حركة شهيق في 60 ثانية، 14 حركة شهيق في 15 ثانية
المعدلان غير متناسبين لأنه لا يوجد عدد صحيح يقسم عليه 16 لينتج 14 ليصبح البسط بسيط في حين أن المقام قسم على 4، المعدلان غير متناسيين
دراسة مسحية: لوحظ أن 3 طلاب من بين 5 طلاب في مدرسة الصديق يشترون شطائر من المقصف، و أن 12 طالباً من بين 19 طالباً في مدرسة الفاروق يفعلون ذلك، فهل هذه النتائج متناسبة؟ فسر إجابتك
النسب ليست متناسية لأن كل منهما في أبسط صورة له وغير متساويين، النسبتين غير متناسبين
فصل النسبة المئوية و الاحتمالات
خمن: كيف يمكنك أن تحول النسبة المئوية إلى كسر اعتيادي؟ و كيف يمكنك أن تحول الكسر الاعتيادي الذي مقامه 100 إلى نسبة مئوية؟
اكتب العدد الذي يسبق إشارة النسبة المئوية فى البسط و اكتب العدد 100 في المقام
اكتب يسط العدد و أتبعه بإشارة النسبة المئوية
اكتب: هل العبارة الآتية صواب أم خطأ، و فسر إجابتك. و إذا كانت خاطئة فأعط مثالاً مضاداً:
(عند كتابة عدد أكبر من 1 في صورة نسبة مئوية، يجب أن تكون إحدى النسب في التناسب كمية غير معلومة منسوبة إلى 1000)
العبارة خاطئة، حيث أن في النسب المنوية تكون النسبة منسوبة إلى 100 وليس 1000، بغض النظر عن كون الكسر أكبر من 1 أو أقل منه، مثال: عند كتابة 180%
180% = 180 /100 = 9 /5
تمرين: أرادت مريم عمل منظر من ملصقات للنجوم، يتكون من 10 صفوف، فوضعت نجمة في الصف الأول و 3 نجمات في الصف الثاني و 5 نجمات في الصف الثالث، و هكذا استمرت بهذا النمط، فكم نجمة ستكون في الصف السابع؟
افهم: قامت مريم بعمل منظر من ملصقات النجوم يتكون من ١٠ صفوف وضعت في الصف الأول نجمة و الثاني 3 نجمات والثالث 5 نجمات
المطلوب: عدد النجمات في الصف السابع
خطط: ابحث عن نمط لإيجاد عدد النجمات
حل: استعمل جدولاً لإيجاد النمط

عدد النجمات فى الصف السايع هي 13 نجمة
اكتب: شرحاً للعلاقة بين احتمال حادثة و احتمال متممتها، ثم أعط مثالاً على ذلك.
احتمال الحادث = عدد النواتج في الحادثة / العدد الكلي للنواتج الممكنة
و لكن احتمال متممتها = ح (الحدث) + ح (عدم وجود الحدث)
و من هنا ينتج أن حدوث الحادثة أو متممتها أمر مؤكد الحدوث
مثال: إذا كان احتمال سقوط المطر فاحتمال المتممة و هي عدم سقوط المطر هو 70 %
و من المؤكد أن أحد هذين الأمرين سوف يتحقق
تمرين: أوجد الاحتمال التجريبي لمحاولات طلاب الصف جميعهم، ثم قارن بين الاحتمال التجريبي و الاحتمال النظري
يقوم طلاب صفي بعمل نفس التجربة و تدون النتيجة و سوف تكون النسب أكثر قرباً إلى قيمة الاحتمال التجريبي الذي حصلت عليه كل مجموعة وحدها
خمن: اشرح لماذا يمكن أن يكون الاحتمال التجريبي الذي حصلت عليه أقرب إلى الاحتمال النظري من الاحتمال التجريبي
كلما زاد عدد المحاولات اقترب الاحتمال التجريبي أكثر فأكثر من الاحتمال النظري
اجمع البيانات: اعمل مع زميلك، و اطلب إليه أن يضع أعداداً مختلفة من المكعبات الجمراء و المكعبات الزرقاء في الكيس على أن يكون مجموعها 10، و استعمل الاحتمال التجريبي لتخمن العدد الصحيح من المكعبات الحمراء و المكعبات الزرقاء في الكيس، ثم برر إجابتك
نضع 10 مكعبات في كيس و نبدأ بالسحب، سنجد أنه يتم سحب مكعب أحمر ثم مكعب أزرق على التوالي ويكون الفرض المتوقع أن الكيس يحتوي على عدد من المكعبات الزرقاء مساوي لعدد المكعبات الحمراء
فصل الهندسة: الزوايا و المكعبات
تمرين: استعمل المنقلة و المسطرة لرسم كل من الزوايا التي لها القياسات التالية:
1- 68 ْ
الخطوة 1: ارسم أحد ضلعي الزاوية، ثم حدد رأسها
الخطوة 2: ضع المنتقلة حيث ينطبق مركزها على نقطة رأس الزاوية و تكون الإشارة المقابلة للصفر على استقامة واحدة مع ضلع الزاوية ثم ابحث عن الزاوية المراد رسمها على التدريج المناسب؛ و عين نقطة بمحاذاته على الورقة
الخطوة 3: ارفع المنقلة ثم صل بين رأس الزاوية والنقطة التي عينها مستعملاً المسطرة
2- 105 ْ
الخطوة 1: ارسم أحد ضلعي الزاوية، ثم حدد رأسها
الخطوة 2: ضع المنتقلة حيث ينطبق مركزها على نقطة رأس الزاوية و تكون الإشارة المقابلة للصفر على استقامة واحدة مع ضلع الزاوية ثم ابحث عن الزاوية المراد رسمها على التدريج المناسب؛ و عين نقطة بمحاذاته على الورقة
الخطوة 3: ارفع المنقلة ثم صل بين رأس الزاوية والنقطة التي عينها مستعملاً المسطرة
3- 85 ْ
الخطوة 1: ارسم أحد ضلعي الزاوية، ثم حدد رأسها
الخطوة 2: ضع المنتقلة حيث ينطبق مركزها على نقطة رأس الزاوية و تكون الإشارة المقابلة للصفر على استقامة واحدة مع ضلع الزاوية ثم ابحث عن الزاوية المراد رسمها على التدريج المناسب؛ و عين نقطة بمحاذاته على الورقة
الخطوة 3: ارفع المنقلة ثم صل بين رأس الزاوية والنقطة التي عينها مستعملاً المسطرة
4- 25 ْ
الخطوة 1: ارسم أحد ضلعي الزاوية، ثم حدد رأسها
الخطوة 2: ضع المنتقلة حيث ينطبق مركزها على نقطة رأس الزاوية و تكون الإشارة المقابلة للصفر على استقامة واحدة مع ضلع الزاوية ثم ابحث عن الزاوية المراد رسمها على التدريج المناسب؛ و عين نقطة بمحاذاته على الورقة
الخطوة 3: ارفع المنقلة ثم صل بين رأس الزاوية والنقطة التي عينها مستعملاً المسطرة
5- 140 ْ
الخطوة 1: ارسم أحد ضلعي الزاوية، ثم حدد رأسها
الخطوة 2: ضع المنتقلة حيث ينطبق مركزها على نقطة رأس الزاوية و تكون الإشارة المقابلة للصفر على استقامة واحدة مع ضلع الزاوية ثم ابحث عن الزاوية المراد رسمها على التدريج المناسب؛ و عين نقطة بمحاذاته على الورقة
الخطوة 3: ارفع المنقلة ثم صل بين رأس الزاوية والنقطة التي عينها مستعملاً المسطرة
5- 60 ْ
الخطوة 1: ارسم أحد ضلعي الزاوية، ثم حدد رأسها
الخطوة 2: ضع المنتقلة حيث ينطبق مركزها على نقطة رأس الزاوية و تكون الإشارة المقابلة للصفر على استقامة واحدة مع ضلع الزاوية ثم ابحث عن الزاوية المراد رسمها على التدريج المناسب؛ و عين نقطة بمحاذاته على الورقة
الخطوة 3: ارفع المنقلة ثم صل بين رأس الزاوية والنقطة التي عينها مستعملاً المسطرة
فصل القياس المحيط و المساحة و الحجم
تخمين: كيف يمكنك أن تجد المسافة حول دائرة ما إذا عرفت المسافة بين مركزها و نقطة تقع عليها؟
نضاعف المسافة بين المركز والنقطة ونقيسها بالمسطرة السنتيمترية ونضع خيط بنفس الطول فيكون هو القطر ونلف حوله خيط آخر بحيث يلتقي مع أطراف الخيط الأول ونقيس طول الخيط الآخر، أو أضرب المسافة في 2 لإيجاد قطر الدائرة؛ ثم أضرب الناتج في 3 لتقدير المحيط




