حل كتاب الرياضيات الفصل الثاني للصف الخامس الابتدائي للعام الدراسي 1447، كتاب الرياضيات حسب المناهج المملكة العربية السعودية، كتاب الرياضيات ف2 خامس ابتدائي متوفر على موقع حلول
حل كتاب الرياضيات خامس ابتدائي
حل الفصل الخامس العبارات الجبرية والمعادلات
حل الفصل السادس الكسور الاعتيادية
فصل الإحصاء و الاحتمال
تمرين: من المتوقع أن يلتقي أحمد بأبناء عمه يوم الجمعة أو يوم السبت، و يذهبون لزيارة جدهم أو عمتهم، صف موقفين مختلفين يمكن أن يحدثا.
يمكن أن يخرج أحمد مع أصدقاءه يوم الخميس ويذهبوا إلى مطعم و يمكن أن يخرج أحمد مع أصدقائه يوم الخميس و يذهبوا إلى الحديقة العامة
تحدث: صف خطوات إيجاد الوسيط لمجموعة من البيانات.
رتب البيانات من الأصغر إلي الأكبر
إذا كان عدد البيانات فردي فالقيمة الواقعة في الوسط هي الوسيط
إذا كان عدد البيانات زوجي فالوسيط هو ناتج قسمة مجموع القيمتين الواقعتين في الوسط على 2
اكتب: إذا كان وسيط أطوال زملائك في الصف 125 سنتمتراً، فماذا تستنتج من ذلك؟ فسر إجابتك.
أستنتج من ذلك أن متوسط طول الزملاء هو 125 سم أي يقع في الوسط أي هناك عدد من الزملاء طولهم أكبر من 125 سم يساوي عدد الزملاء طولهم أقل من 125 سم
تمرين: تسابق أربعة أصدقاء، فأنهى خالد السباق بعد أحمد و قبل سعد، و أنهى عبد اللطيف السباق بعد خالد و قبل سعد، من الفائز في السباق؟
افهم: في سباق أنهى خالد السباق بعد أحمد و قبل سعد؛ وأنهى مروان بعد خالد و قبل سعد، المطلوب: من الفائز في السباق؟
خطط: استعمل خطة إنشاء جدول لأجد حل المسألة
حل: خالد بعد أحمد و قبل سعد؛ إذاً الترتيب أحمد؛ خالد؛ سعد
مروان بعد خالد و قبل سعد؛ إذاً الترتيب خالد؛ مروان، سعد
إذاً الفائز في السباق هو أحمد
تمرين: تحتاج وصفة لعمل الكعك إلى كوب من عصير البرتقال و كوبين من الدقيق، لكن أماني تريد أن تصنع كمية أكبر من الكعك، إذا استعملت 6 أكواب من الدقيق، فكم كوباً من عصير البرتقال تحتاج؟
افهم: تحتاج وصفة لعمل الكعك إلى كوب من عصير البرتقال و كوبين من الدقيق؛ تريد أماني أن تصنع كمية أكبر من الكعك. استعملت 6 أكواب من الدقيق، المطلوب: كم كوب برتقال تحتاج؟
خطط: استعمل خطة تمثيل المعطيات لأجد حل المسألة
حل: عدد الكعكات = عدد أكواب الدقيق ÷ عدد أكواب الكعكة الواحدة
= 6 ÷ 2 = 3 كعكات
عدد أكواب البرتقال = عدد الكعكات × عدد أكواب الكعكة الواحدة
= 3 × 1 = 3 أكواب
تمرين: يبين الجدول أدناه عدد الشطائر التي أعدها مقصف المدرسة في 11 يوماً، إذا كان أحد الأيام غير معلوم، و كان الوسيط للأعداد 20، و يوجد أكثر من منوال، فأوجد قيمة متوقعة للعدد في اليوم غير المعلوم
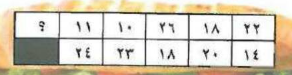
افهم: أعد مقصف مدرسة شطائر في ١١ يوماً؛ و كان عدد الشطائر في أحد الأيام غير معلوم؛ و الوسيط لعدد الشطائر 20، و يوجد أكثر من منوال، المطلوب: ما القيمة المتوقعة للعدد الغير معلوم؟
خطط: رتب عدد الشطائر وحدد الوسيط و المنوال
حل: ترتيب عدد الشطائر: 10 - 11 - 14 - 18 - 18 - 20 - 22 - 23 - 24 - 26
بما أن الوسيط 20 إذا العدد الغير معلوم أكبر من 20
بما أن يوجد أكثر من منوال، إذا العدد الغير معلوم يجب أن يكون منوال
العدد الغير معلوم يمكن أن يكون 20 - 22 - 23 - 24 - 26
تمرين: إذا كان وسيط أطوال زملائك في الصف 125 سنتمتراً، فماذا تستنتج من ذلك؟ فسر إجابتك
أستنتج من ذلك أن متوسط طول الزملاء هو 125 سم أي يقع في الوسط أي هناك عدد من الزملاء طولهم أكبر من 125 سم يساوي عدد الزملاء طولهم أقل من 125 سم
تمرين: في حصالة ياسر 40 ريال، و في حصالة أخيه عماد 35 ريال، إذا ادّخر عماد 5 ريالات كل أسبوع، و ادّخر ياسر 4 ريالات كل أسبوع، فبعد كم أسبوع يتساوى ما في الحصالتين؟
افهم: في حصالة حمود 40 ربإل؛ و في حصالة عماد 35 ريال؛ إذا ادّخر عماد 5 ريالات كل أسبوع؛ وأدخر حمود 4 ريالات كل أسبوع، المطلوب: بعد كم أسبوع يتساوى الحصالتين؟
خطط: استعمل خطة إنشاء جدول لأجد حل المسألة
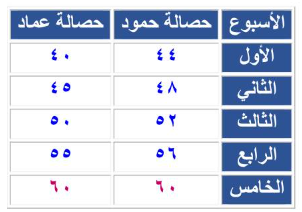
حل: يتساوى الحصالتين في الأسبوع الخامس
تمرين: دعا فارس 7 أشخاص من أقاربه إلى العشاء، و طلب إلى كل منهم أن يصافح الضيوف الآخرين، كم مرة سيصافح الضيوف بعضهم بعضاً؟
افهم: دعا فارس 7 أشخاص إلى العشاء و طلب من كل منهم أن يصافح الضيوف الآخرين، المطلوب: كم مرة يصافح الضيوف بعضهم بعضاً؟
خطط: استعمل خطة تمثل المعطيات لأجد حل المسألة
عدد الأشخاص 7، إذا كل منهم يصافح 6 أشخاص آخرين مع الأخذ في الاعتبار عدم التكرار أي إذا صافح الأول الثاني؛ لا نحسب مصافحة الثاني للأول لأنها حسبت من قبل
حل: الأول سيصافح 6 أفراد - الثاني 5 أفراد - الثالث 4 أفراد - الرابع 3 أفراد - الخامس 2 فردين - السادس 1 فرد - السابع تم المصافحة للجميع من قبل
عدد مرات التصافح = 6 + 5 + 4 + 3 + 2 + 1 = 21 مرة
اكتب: اسم الخطة التي استعملتها لحل المسألة السابقة و بين لماذا تعد هذه الخطة مناسبة لحل المسألة؟
التمثيل، يمكن إيجاد عدد المصافحات الكلية بأن يقوم الاأشخاص السبعة بمصافحة كل منهم الآخر.
عدد الأشخاص 7؛ إذا كل منهم يصافح 6 أشخاص آخرين مع الأخذ في الاعتبار عدم التكرار أي إذا صافح الأول الثاني؛ لا نحسب مصافحة الثاني للأول لانها حسبت من قبل
تحدث: شرح خطوات إنشاء تمثيل بالأعمدة المزدوجة.
رسم المحورين الأفقي و الرأسي واضع عنوانا لكل منهما
حدد مقياس التدرج و الفترات
اكتب مفتاحاً للأعمدة ليوضح نوع كل عمود
اكتب عنواناً للتمثيل
ارسم أعمدة بحسب الأطوال المناسبة تمثل البيانات
اكتب: مسألة من واقع الحياة يمكن حلها بوصف الاحتمالات ثم حل المسألة
هناك كيس به 10 بلورات؛ 6 بلورات حمراء؛ 3 بلورات صفراء؛ بلورة زرقاء
سحب بلورة حمراء احتمال قوي
سحب بلورة صفراء احتمال ضعيف
سحب بلورة سوداء احتمال مستحيل
فصل القواسم و المضاعفات
اكتب: لماذا لا يكون وقوف 24 طالباً في صف واحد خياراً جيداً للتصوير معاً؟
لا يكون وقوفهم في صف واحد خيار جيد للتصوير لأنهم سيكونوا أكبر من عرض الكاميرا
تحدث: وضح خطوات إيجاد القاسم المسترك الأكبر لعددين، و أعط مثالاً على ذلك
أكتب أولا قواسم كل عدد؛ ثم أحدد القواسم المشتركة للعددين، إن أكبر هذه القواسم هو القاسم المشترك الأكبر (ق. م. أ)
مثال: القاسم المشترك الأكبر للعددين 6 و 8
قواسم العدد 6 : 1 - 2 - 3 - 6
قواسم العدد 8: 1 - 2 - 4 - 8
(ق.م.أ) = 2
تمرين: تريد ليلى أن تضع 16 برتقالة و 20 تفاحة و 24 حبة كمثرى في سلال بحيث يكون في كل سلة العدد نفسه من كل نوع، فما أكبر عدد من السلال تستطيع ليلى ترتيبها؟ و ما عدد التفاحات في كل منها؟
بإيجاد القواسم لكل من 16 - 20 - 24 ثم إيجاد القواسم المشتركة و نجد منها أن أكبر عدد مشترك بينهم هو 4، و عدد التفاحات في كل منهما = 20 / 4 = 5
4 سلال - 5 تفاحات
تمرين: يريد بستاني أن يزرع 27 وردة بنفسج، و 36 وردة نرجس في صفوف بحيث يكون في كل صف العدد نفسه من كل نوع، ما أكبر عدد من الصفوف يمكن للبستاني أن يزرعها؟ و ما عدد وردات البنفسج في كل صف؟
أكبر عدد من الصفوف يمكن أن يزرعها البستاني هو القاسم المشترك الأكبر للعددين 27 و 36 و هو 9, أما عدد وردات البنفسج في كل صف هو 27 / 9 = 3
9 صفوف - 3 وردات
مسألة مفتوحة: اكتب عددين قواسمهما المستركة 1 - 3 - 5، و بين كيف وجدت العددين
أجد أولاً ناتج 1 × 3 × 5 لأحصل على العدد الأول 15 ثم أضرب في عدد آخر مثل 2 لأحصل على العدد الثاني، في هذه الحالة؛ يكون العدد الثاني 30، و كلا العددين لهما القواسم 1 - 3 - 5 نفسها
اكتب: هل يمكن أن يكون القاسم المشترك الأكبر لععدين هو 1؟ فسر إجابتك و ادعمها بمثال.
نعم؛ عندما يكون العدد ١ هو القاسم المشترك الوحيد للعددين فهو القاسم المشترك الأكبر لهما، مثال: القاسم المشترك الأكبر للعددين 5 و 7 و ذلك لأن العدد ١ هو القاسم المشترك الوحيد لهذين العددين
فصل جمع الكسور و طرحها
اكتب: مسألة من واقع الحياة يمكن حلها بجمع كسور متشابهة، ثم حل المسألة
المسألة: ذهب محمد إلى المدرسة فقطع مسافة 1 / 2 في الذهاب؛ و قطع نفس المسافة في العودة؛ أوجد المسافة الكلية للذهاب و العودة؟
الحل: المسافة الكلية للذهاب و العودة = 1 /2 + 1 /2 = 2 /2 = 1 متراً
اكتب: كيف تجد ناتج 9 /12 - 4 /12 دون استعمال نماذج الكسور؟
اطرح البسطين و نكتب الناتج على المقام نفسه
تمرين: كيف يساعدك إيجاد مضاعفات العددين 4 - 12 على إيجاد ناتج 3 /4 + 7 /12
يساعدني على إيجاد نموذج يطابق طول النموذجين المطلوبين بما أن 12 هو المضاعف المشترك الأصغر (م. م. أ) للمقامين 4 - 12 لذا فهو المقام المشترك الأصغر للكسرين 3 /4 - 7 /12
اكتب: مسألة من واقع الحياة يتطلب حلها جمع كسور غير متشابهة
أخذ محمد مسافة 1 /2 كيلو متر إلى الحديقة و مسافة 1 /3 كيلو متر إلى النادي، أوجد مجموع ما مشاه محمد؟
اكتب: مسألة من واقع الحياة يمكن حلها بطرح كسرين غير متشابهين
اشترى محمد 1 /2 كيلو جرام من اللحم؛ 1 /4 كيلو جرام من الدجاج. ما مقدار الزيادة في كمية اللحم عن كمية الدجاج؟
فكر: يصل طول أنثى ضفدع الأشجار الكوبية إلى 1 /8 متر، أما ذكر هذا النوع من الضفادع فيصل طوله إلى 3 /40 من المتر، فكم يزيد طول الأنثى عن طول الذكر؟
1 /8 - 3 /40 = 16 /320 = 0.05
فصل وحدات القياس
فكر: أيهما أسهل قياس الأشياء إلى أقرب سنتمتر أم قياس أقرب ملمتر؟ وضح إجابتك
الأسهل القياس لأقرب سنتيمتر أكبر من المليمتر
فكر: أيهما أكثر دقة قياس شيء إلى أقرب سنتمتر أم إلى أقرب ملمتر؟ برر اختيارك
القياس إلى أقرب مليمتر أدق لأن الملمتر أصغر من السنتمتر (تزداد دقة القياس كلما صغرت وحدة القياس)
اكتب: هل تقيس طول دراجة هوائية بالسنتمترات أم بالملمترات؟ برر اختيارك
أقيسها بالسنتيمتر؛ لأنه الأنسب لقياسها
اكتب: كيف تختار الوحدة المترية المناسبة عند قياس طول شيء ما؟ و ادعم إجابتك بأمثلة
أبعاد الشيء تحدد الوحدة التي تستخدم، فمثلا لقياس جسم صغير مثل قلم تستخدم وحدة صغيرة مثل السنتيمتر لقياس جسم كبير مثل بيت فإنك تستخدم وحدة المتر و لقياس مسافة كبيرة جدا تستخدم وحدة الكيلومتر
اكتب: مسألة من واقع الحياة، و اجعل لها إجابة غير معقولة، ثم بين السبب في عدم معقولية الحل
قدر باسم أنه يحتاج إلى سلم طوله متر واحد ليصل إلى سطح منزله المكون من طابقين، هل هذا معقول؟ وضح.
الإجابة: لا؛ لأن ارتفاع المنزل 5 أمتار على الأقل
فصل الأشكال الهندسية
تحدث: وضح الفرق بين نصف المستقيم و المستقيم
نصف المستقيم له نقطة بداية و ليس له نقطة نهاية؛ المستقيم ليس له نقطة بداية و لا نقطة نهاية
تمرين: اذكر شيئاً من غرفة الصف يحوي مستقيمات متوازية، ثم اذكر شيئاً آخر يحوي مستقيمات متعامدة
الحافتان المتقابلتان للنافذة متوازيتان
الحافة الجانبية و الحافة السفلية للسبورة متعامدتان
اكتب: مقارنة بين المستقيمات المتعامدة و المستقيمات المتوازية
المستقيمات المتعامدة تتقاطع لكنها تشكل زاوية قائمة
المستقيمات المتوازية لا يمكن أن تلتقي
تمرين: بين متى تستعمل خطة الاستدلال المنطقي لحل المسائل
عندما يكون لديك مجموعة من الحقائق ترشدك إلى النتيجة أو عندما تستطيع حذف بعض المعلومات التي تساعدك في التوصل إلى حل للمسألة
تمرين: شارع الجامعة و شارع البلدية لا يلتقيان أبداً، و المسافة بينهما متساوية دائماً، أما شارع العروبة فيقطع الشارعين مشكلاً زوايا قائمة، كما يحاذي شارع العروبة شارع النادي و لا يقطعه، أي الشوارع متعامدة؟
افهم: معطيات المسألة:
شارع الجامعة وشارع البلدية لا يلتقيان أبداً، المسافة بينهما متساوية دائماً
شارع العروبة يقطع الشارعين مشكلاً زوايا قائمة؛ و يحاذي شارع العروبة شارع النادي و لا يقطعه، المطلوب: أي الشوارع متعامدة
خطط: استعمل خطة الاستدلال المنطقي
حل: شارع الجامعة متعامد مع شارع العروبة و النادي؛ و شارع البلدية متعامد مع شارع العروبة و النادي
تحقق: تحقق من المعطيات، إذن الإجابة صحيحة
فصل المحيط و المساحة و الحجم
اكتب: مسألة من واقع الحياة يمكن حلها بإيجاد المحيط، ثم حل المسألة
يزرع شخص أزهارا حول حديقة مستطيلة الشكل طولها 8 م و عرضها 5 م، فإذا أراد أن يجد محيط الحديقة ليحدد عدد الأزهار التي سيزرعها، فما محيط الحديقة؟
المحيط = 26 م
تحدث: صف طريقة واحدة لتقدير مساحة شكل غير منتظم مرسوم على ورقة مربعات
الطريقة هي: نقوم بعد المربعات الكاملة و أنصاف المربعات ثم الجمع
تحدث: ما الفرق بين الأسطوانة و المنشور الرباعي؟
الأسطوانة فيها دائرتين متطابقتين و متوازيتان
أما المنشور الرباعي فيه كل وجهان متقابلان متطابقان و متوازيان و كل ضلعان متجاوران متعامدان
تحدث: ما الوحدات المناسبة لقياس حجم صندوق مجوهرات؟ هل من المعقول استعمال الوحدات نفسها لقياس حجم موقف السيارات؟ فسر إجابتك
السنتيمتر المكعبة مناسبة؛ لأن العلبة صغيرة، و لكن ليس من المعقول استعمال السنتيمترات المكعبة لقياس حجم موقف سيارت؛ لأن موقف السيارات كبير، و لذلك يكون أكثر معقولية استعمال الأمتار المكعبة لقياس حجم موقف السيارات






لاكن الاحلام طويل بس يا ريت يصير في اختيار.
و شكرا