حل كتاب الرياضيات للصف الرابع الابتدائي الفصل الثاني للعام الدراسي 1447، كتاب الرياضيات ف2 يتضمن حل التمارين و النشاطات، كتاب الرياضيات التابع للمناهج الجديدة في المملكة العربية السعودية
حل كتاب الرياضيات رابع ابتدائي
حل الفصل الخامس الضرب في عدد من رقم واحد
حل الفصل السادس الضرب في عدد من رقمين
فصل القسمة على عدد من رقم واحد
تمرين: يحتوي كتاب أحمد على 81 صفحة، إذا قرأ منها 38 صفحة، فكم صفحة بقيت دون قراءة؟
81 - 38 = 43 صفحة
أطرح عدد الصفحات التي قرأها أحمد من عدد صفحات الكتاب كله
تمرين: مع عمر 32 ريالاً، و يريد شراء ألعاب إلكترونية، إذا كان ثمن اللعبة الواحدة 8 ريالات، فكم لعبة يمكنه أن يشتري؟
أقسم ما مع عمر من ريالات على ثمن اللعبة الواحدة 32 ÷ 8 = 4 لعب
تمرين: بلغ عدد زوار الحيوانات يوم الخميس 2515 شخصاً، و يوم الجمعة 3496 شخصاً، ما عدد الزوار في اليومين تقريباً؟
عدد الزوار في اليومين = 2515 + 3496 = 6011 زائر = 6000 زائر تقريبا
تمرين: كيف تستعمل قطع النماذج لتجد ناتج 58 ÷ 4؟
الخطوة 1: مثل المقسوم 58 باستعمال قطع النماذج؛ استعمل 8 آحاد و 5 عشرات لتمثيل 58
الخطوة 2: قسم العشرات: المقسوم عليه هو 4؛ إذن قسم العشرات إلى 4 مجموعات بالتساوي؛ فتحصل على عشرة في كل مجموع و يتبقى 10 واحدة
الخطوة 3: قسم الآحاد أعد تجميع العشرة إلى ١٠ آحاد؛ ثم قسم الآحاد على 4 مجموعات بالتساوي فتحصل على 4 آحاد و عشرة واحدة في كل مجموعة؛ و يتبقى 2 أحاد تسمى الباقي
إذن 58 ÷ 4 = 14 و الباقي 2
تمرين: فسر ما يعنيه وجود باق عند القسمة.
عند قسمة عددين أحيانا يتبقى عدد أصغر من المقسوم عليه لا يقبل القسمة على المقسوم عليه مرة أخرى؛ هذا العدد يسمي بالباقِ
تمرين: استعمل قطع النماذج للقسمة في كل مما يلي:
36 ÷ 2
الخطوة 1: مثل المقسوم 36 باستعمال قطع النماذج - استعمل 6 آحاد و 3 عشرات لتمثيل 36
الخطوة 2: قسم العشرات: المقسوم عليه هو 2، إذن قسم العشرات إلى 2 مجموعة بالتساوي ؛ فتحصل على عشرة واحدة في كل مجموعة و تبقى عشرة
الخطوة 3: قسم الآحاد: أعد تجميع العشرة إلى ١٠ آحاد؛ ثم قسم الآحاد على المجموعات الاثنين بالتساوي فتحصل على 8 أحاد و عشرة واحدة في كل مجموعة، أي ما يساوي 18
تمرين: كيف تستعمل قطع النماذج لتجد ناتج 79 ÷ 6
الخطوة 1: مثل المقسوم 79 باستعمال قطع النماذج - استعمل 9 آحاد و 7 عشرات لتمثيل 79
الخطوة 2: قسم العشرات: المقسوم عليه هو 6، إذن قسم العشرات إلى 6 مجموعات بالتساوي؛ فتحصل على عشرة واحدة في كل مجموعة و تبقى عشرة
الخطوة 3: قسم الآحاد: أعد تجميع العشرة إلى ١٠ أحادء ثم قسم الآحاد على 6 مجموعات بالتساوي؛ فتحصل على 3 آحاد و عشرة واحدة في كل مجموعة؛ أي ما يساوي 13 والباقي 1
تحدث: لماذا يكون الباقي دائماً أقل من المقسوم عليه؟
لأنه لو كان مثله أو أكبر منه لقبل القسمة عليه
اكتب: حينما تقسم عدداً على 6، فهل يمكن أن يكون الباقي 6؟ فسر إجابتك
لا يمكن لأن الباقي يجب دائما أن يكون أصغر من المقسوم عليه؛ لأنه لو كان مثله أو أكبر منه لقبل القسمة عليه
اكتب: كيف تعرف أن ناتج قسمة 600 ÷ 2 يتكون من 3 أرقام
لأن العدد 600 يتكون من آحاد و عشرات و مئات و المئات يقبل القسمة على 2 فيكون الناتج مكون من أرقام و يكون الناتج = 300
تمارين:
1- قرأت سلمى 75 صفحة من كتاب في خمسة أيام، إذا كانت تقرأ العدد نفسه كل يوم، فكم صفحة قرأت في اليوم الواحد؟
15
2- ذهب حمد إلى حفل تخرج أخيه من الجامعة، و كان هناك 1200 خريج قد اصطفوا في 4 صفوف متساوية، فكم طالباً في الصف الواحد؟
300
3- قسمت المعلمة 35 طالبة في 7 مجموعات بالتساوي، فكم طالبة في كل مجموعة؟
35 ÷ 7 = 5
إذن يوجد 5 طالبات في كل مجموعة
4- بدأ 6 طلاب كتابة تقارير عن 27 معلماً سياحياً في المملكة إذا اقتسموا الكتابة عن هذه المعالم بالتساوي، فكم تقريراً سيكتب كل منهم؟ و كم طالباً سيكتب تقريراً إضافياً؟
27 ÷ 6 = 4 و الباقي 3
سيكتب كل طالب 4 تقارير؛ و سيكتب 3 طلاب تقريراً إضافياً
5- فسر لماذا استعملنا:
هدية + هدية + (هدية + 3 ريالات) لحل المسألة السابقة
لأن هناك هديتان متساويتان في التكلفة؛ أما الهدية الثالثة تزيد كلفتها على كل من الهديتين الأخريين ب 3 ريالات
6- لماذا كان التخمين الأول 9 ريالات، و لم يكن عدداً أقل؟ اشرح
لأن 9 هو أقل عدد بعد 10 ريالات، لأن 10 × 3 = 30 ريال، و التكلفة الكلية 27 ريالاً و لأن 27 ÷ 3 = 9 ريالات
7- الجبر: يهوى كل من عبد الله و يوسف جمع الطوابع، إذا كان عدد الطوابع التي جمعاها معاً 249 طابعاً، حيث جمع يوسف طوابع أقل من عبد الله بـــ 37 طابعاً، فكم طابعاً جمع كل منهما؟
أفهم: معطيات المسألة: عند عبد الله أكثر من 37 طابع
عند يوسف أقل مما عند عبد الله ب 37 طايعاً
مجموع ما عند يوسف وعبد الله 249 طابعاً
المطلوب: إيجاد كم طابع عند يوسف وكم طابع عند عبد اللّه
خطط: باستعمال خطة التخمين والتحقق لحل المسألة
حل: ما عند عبد الله + ما عند يوسف = 249 طابعاً
100 + (100 - 37) = 163
130 + (130 - 37) = 223
140 + (140 - 37) = 243
145 + (145 - 37) = 253
144 + (144 - 37) = 251
143 + (143 - 37) = 249
إذن عند عبد الله 143 طابع و عند يوسف 106 طابع
تحقق: 143 + 106 = 249 طابعاً
فصل الأشكال الهندسية و الاستدلال المكاني
تحدث: إذا قُصت ورقة رباعية الشكل إلى أي قطعتين، فما اسما الشكلين الناتجين؟
إذا قصت ورقة رباعية الشكل طولياً تعطي شكلين رباعيين الشكل؛ أما إذا قصت من القطر تعطي شكلين مثلثين
اكتب: اكتب أسماء ثلاثة أشياء من حولك تظهر فيها مضلعات
تظهر المضلعات من حولنا في الورق شكل رباعي المثلث من أدوات الهندسة؛ المكتب، الدفتر
تمرين: أكمل الجدول التالي، ما النمط الذي تراه؟
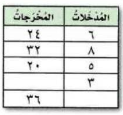
افهم:
تعرف على النمط الموجود في الجدول
تعلم كيف تصل الأرقام في الجدول إلى هذا الترتيب
احسب الأعداد الناقصة لتكملة النمط في الجدول
خطط: ابحث عن النمط في الجدول لتكملة الأرقام الناقصة
حل: نلاحظ معدل الزيادة في ا لأرقام في الجدول في كل خانة
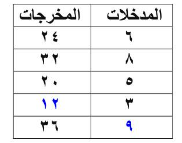
نجد أن الزيادة ثابتة و نحصل عليها من ضرب العدد في 4؛ لنجد أن الجدول يصبح كالآتي:
تمرين: تصل مها إلى المطار في أول طائرة تهبط بعد الساعة 8 صباحاً، إذا علمت أن هناك طائرة تصل كل 45 دقيقة بعد الساعة 6 صباحاً، فمتى تصل طائرة مها؟
افهم: يصل محمد في أول طائرة بعد الساعة الثامنة
هناك طائرة تصل كل 45 دقيقة بعد الساعة السادسة
اعرف ميعاد وصول طائرة محمد
خطط: اعرف النمط لهبوط الطائرات وحدد ميعاد طائرة محمد
حل: هناك طائرة تهبط كل 45 دقيقة من بعد الساعة السادسة
إذن النمط يبدأ من الرقم 6 و يستمر بزيادة 45 دقيقة ليصبح النمط كالآتي:
6:45 - 7:30 - 8:15
إذن أول طائرة تصل بعد الساعة الثامنة هي طائرة محمد التي تصل الساعة 8:15
اكتب: أنشئ نمطاً هندسياً ثم اعرضه أمام الصف، و اطلب من أحد زملائك أن يكمله
أفترض نمطاً هندسياً وليكن مريع ثم خماسي ثم مثلث
نكمل التسلسل على نفس النمط السابق
تحدث: متى تكون الزاوية حادة، أو منفرجة، أو قائمة؟
تكون الزاوية حادة إذا كان قياسها أكبر من الصفر وأقل من 90 ْ
تكون الزاوية قائمة إذا كان قياسها يساوي 90 ْ
تكون الزاوية منفرجة إذا كان قياسها أكبر من 90 ْ وأقل من 180 ْ
اكتب: اختر ثلاثة أشياء في صفك فيها زوايا ثم صنف كل زاوية إلى حادة أو منفرجة أو قائمة
الزاوية المنفرجة: عقارب الساعة عند الساعة الرابعة
الزاوية القائمة: زاوية تصنعها ضلعي المنضدة
الزاوية الحادة: فرجار يرسم دائرة صغيرة
اكتب: هل يمكن أن يكون الشكل مضلعاً و ثلاثي الأبعاد؟ فسر إجابتك
لا؛ لا يمكن أن يكون الشكل مضلعا و ثلاثي الأبعاد؛ لأن الشكل الثلاثي الأبعاد هو مجسم له طول و عرض و ارتفاع و أما المضلعات هي أشكال مستوية مغلقة، لها ثلاث قطع مستقيمة أو أكثر تسمى أضلاعاً و ليس لها ارتفاع
تحدث: إذا كان مجموع طولي ضلعي مثلث متطابق الأضلاع 6 سم، فما طول الضلع الثالث؟ اشرح إجابتك.
بما أن المثلث متطابق الأضلاع؛ إذاً فجميع أضلاعه متساوية
بما أن مجموع ضلعيه يساوي 6 سم؛ إذاً بقسمة 6 على 2 نحصل على طول الضلع إذاً طول الضلع يساوي 3 سم
بما أنه متطابق الأضلاع، إذاً طول الضلع الثالث يساوي 3 سم
فصل القياس
تمرين: أي الشكلين أطول؟
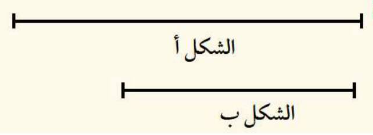
نضع المسطرة عند الصفر على أحد طرفي القطعة المستقيمة و نرى عند أي نقطة، يقع الطرف الثاني من القطعة المستقيمة و هذه النقطة تكون طول القطعة، نكرر نفس الخطوات لقياس القطعة الثانية و نقوم بمقارنة المقاسين أيهما أطول، سنجد أن الشكل (أ) هو الأطول
تمرين: أي الشكلين أطول؟

نضع المسطرة عند الصفر على أحد طرفي المستطيل و نرى عند أي نقطة يقع الطرف الثاني من المستطيل و هذه النقطة تكون طول المستطيل، نكرر نفس الخطوات لقياس المستطيل الثاني و نقوم بمقارنة المقاسين أيهما أطول، سنجد أن الشكل (ب) هو الأطول
تمرين: صنعت مشاعل إطاراً لصورة، إذا كان هذا الإطار مربعاً فكم ضلعاً له الطول نفسه؟
بما أن الإطار مربعاً، إذن يوجد 4 أضلاع لهم الطول نفسه
(من خواص المربع كل أضلاعه متساوية في الطول)
تمرين: اكتب الخطوات التي تقوم بها لقياس الطول باستعمال المسطرة
أضع المسطرة بمحاذاة أحد حافة تلك الأشياء؛ بحيث يقع ال (.) على طرف الحافة ثم أقوم بقياس الشيء لأقرب سنتمتر
فصل الكسور الاعتيادية
تمرين: نسخ حسن على حاسوبه 120 برنامجاً تعليمياً في 10 أيام، إذا كان ينسخ العدد نفسه كل يوم، فكم برنامجاً ينسخ في اليوم الواحد؟
عدد البرامج الذي يقوم بنسخها في اليوم الواحد = 120 ÷ 10 = 12 برنامج
تمرين: تم تقسيم الكعكة إلى 8 أجزاء، إذا أكل محمد جزءاً واحداً و أكل ضيوفه بقية الأجزاء، ما الكسر الذي يمثل الأجزاء التي أكلها الضيوف؟
قم بالطرح عدد الأجزاء كلها ناقص الجزء الذي أكله محمد نحصل على عدد الأجزاء الذي أكلها الضيوف و يكون الناتج هو البسط و عدد الأجزاء كلها هو المقام
8 - 1 = 7
إذن الكسر الذي يمثل الأجزاء التي أكلها الضيوف = 7 / 8
تحدث: ماذا يعني المقام في الكسر؟
المقام هو الرقم تحت خط الكسر و يمثل عدد الأجزاء الكلي
مسألة مفتوحة: اذكر مسألتين مختلفتين من واقع الحياة تستعمل فيهما الكسر 2 / 3
المسألة الأولى: يقوم مزارع بزراعة أرضه بحيث يقوم بزراعة ثلثي الأرض خضروات الكسرالذى يمثل الخضروات = 2 / 3
المسألة الثانية: قامت أم بتقسيم تفاحة على ثلاثة فقامت بإعطاء طفليها جزئين منها و احتفظت بالجزء المتبقي الكسر الذي يعبر عن الجزء الذي أخذه الأطفال = 2 / 3
فصل الكسور العشرية
اكتب: فيم تتشابه الكسور الاعتيادية و الكسور العشرية؟ و فيم تختلف؟
تتشابه في أن كلاهما كسور و كلاهما يمثل جزءاً من الكل
تختلف في أن الكسور العشرية نستخدم فيها الفاصلة أما الكسور الاعتيادية نستخدم فيها علامة القسمة
تحدث: اكتب العدد 0.7 باللمات و وضح ما يعنيه هذا العدد.
سبعة أجزاء من عشرة؛ يعني هذا العدد أن سبعة تمثل جزءاً من كل أي سبعة أجزاء من عشرة أجزاء متطابقة
تحدث: اشرح الفرق بين تعيين 1 / 2 على خط الأعداد، و تعيين نقطة المنتصف بين عددين عليه أيضاً.
نقطة المنتصف بين العددين لا بد أن تقع في منتصف العددين و يمكن أن تكون عدد صحيح أو عدد كسري أما تمثيل على خط الأعداد ليس بالضرورة أن يكون بين عددين و يمكن أن تكون كسر اعتيادي أو كسر عشري
اكتب: كيف تعين العدد 2.5 على خط الأعداد؟
نحدد النقطتان 2 - 3 على خط الأعداد و نضع 2.5 في المنتصف
فصل جمع الكسور العشرية و طرحها
اكتب: أكبر عدد يحتوي منزلة عشرية واحدة و يقرب إلى العدد 75، اشرح كيف وجدت ذلك؟
74.9
حيث أن أكبر عدد في منزلة العشرات هو 9، وبحيث أنه أكبر من 5 فإن 74 تقرب إلى العدد الذي يليها وتصبح 75
اكتب: هل من المعقول أن يكون تقدير ناتج جمع 28.4 + 14.68 يساوي 40
لا، لأن تقدير 28.4 = 28
و تقدير 14.68 = 15
إذن يكون ناتج الجمع يكون 28 + 15 = 43 و ليس 40
اكتب: الخطوات اللازمة لإيجاد ناتج جمع 2.34 + 1.76
مثل الكسر الأول (2.34) بنموذج بتمثيله على شبكتين و 34 مربع من الشبكة الثالثة، ثم الكسر الثاني (1.76) بنموذج بتمثيله على شبكة كاملة و 76 مربع
عد المربعات المظللة لمعرفة ناتج الجمع
تمرين: كيف مثلت ناتج الطرح 2.75 - 1.15؟
مثلت 2.75 بنموذجين و 75 مربع من نموذج ثالث؛ و قمت بشطب شبكة كاملة و 15 مربع من الشبكة الثانية؛ ثم قمت بعد المربعات المتبقية المظللة لأجد ناتج الطرح
- الدرس السابع والعشرون : الضرب في مضاعفات 10 , 100, 1000 صفحة 135
- الدرس الثامن والعشرون : مهارة حل المسألة تقدير معقولية الاجابة صفحة 138
- الدرس التاسع والعشرون : تقدير نواتج الضرب صفحة 140
- الدرس الثلاثون : ضرب عدد من رقمين في عدد من رقم واحد دون اعادة التجميع صفحة 144
- اختبار منتصف الفصل
- الدرس الواحد والثلاثون : ضرب عدد من رقمين في عدد من رقم واحد مع اعادة التجميع صفحة 150
- الدرس الثاني والثلاثون : استقصاء حل المسألة اختبار لحظة المناسبة صفحة 154
- الدرس الثالث والثلاثون : ضرب عدد من ثلاثة أرقام في عدد من رقم واحد صفحة 156
- اختبار الفصل
- الاختبار التراكمي
- الدرس الرابع والثلاثون :الضرب في مضاعفات العشرة صفحة 167
- الدرس الخامس والثلاثون : تقدير نواتج الضرب صفحة 171
- الدرس السادس والثلاثون : خطة حل المسألة تمثيل المسألة صفحة 175
- اختبار منتصف الفصل
- الدرس السابع والثلاثون : ضرب عدد من رقمين في عدد من رقمين صفحة 180
- الدرس الثامن و الثلاثون : ضرب عدد من ثلاثة أرقام في عدد من رقمين صفحة 183
- اختبار الفصل
- الاختبار التراكمي





😊😊😊😊😊😊😊