حل كتاب الرياضيات للصف الثالث ابتدائي الفصل الثاني للعام الدراسي 1447، كتاب الرياضيات في موقع حلول يتضمن حل جميع التمارين و النشاطات الموجودة في كتاب الرياضيات ف2 للثالث ابتدائي.
حل كتاب الرياضيات ثالث ابتدائي
حل الفصل الرابع الضرب 1
حل الفصل الخامس الضرب 2
فصل القسمة (1)
ما القسمة؟
القسمة: عملية تجري بين عددين، أحدهما يمثل عدد الأشياء التي معك، و العدد الآخر يمثل عدد المجموعات المتساوية التي يمكن أن يشكلها
مثال: مع فهد 15 ريال، يريد أن يوزعها على 5 من أصدقائه، فإذا أعطى كلاً منهم العدد نفسه من الريالات فإن كل صديق سيأخذ 15 ÷ 5 أو 3 ريالات
ماذا سأتعلم في هذا الفصل؟
- أستكشف معنى القسمة
- أربط القسمة بالطرح و الضرب
- أقسم على 2، 5، 10
- أستعمل قواعد القسمة، للقسمة مع الصفر و على الواحد
- أكتب جملاً عددية لمسألة القسمة
- أختار العملية المناسبة لحل المسألة
تمرين: تقاسمت هند و سارة و وفاء صندوقاً من الحلوى، أخذت كل واحدة منهن 7 قطع، فكم قطعة حلوى كانت في الصندوق؟
اجمع ما أخذت سارة و هند و وفاء
7 + 7 + 7 = 21
مفهوم القسمة:
القسمة: عملية تجري بين عددين، أحدهما يمثل عدد الأشياء التي معك، و العدد الآخر يمثل عدد المجموعات المتساوية التي يمكن أن يشكلها، فالتقسيم يعني توزيع عدد من الأشياء في مجموعات متساوية لإيجاد عدد المجموعات أو عدد الأشياء في كل مجموعة
أفكر: كيف أقسم 12 قطعة مجموعات متساوية؟ اشرح
ضع 12 قطعة في مجموعات بحيث تكون عدد القطع في كل المجموعات متساوية؛ بحيث كل مجموعة بها 3 قطع
أفكر: كيف أعرف عدد المجموعات المتساوية عندما أقسم القطع مجموعات في كل منها 3 قطع
أعد عدد القطع الموجودة في كل مجموعة؛ أجد أن عدد القطع متساوي في كل المجموعات
تمرين: هل يمكنني تقسيم 13 قطعة بالتساوي إلى مجموعات في كل منها 3 قطع؟ أوضح إجابتي
لدي 13قطعة ويراد توزيعها على مجموعات في كل منها 3 قطع
1- أحضر 13 قطعة؛ و أستعمل أطباق كمجموعات
2- أوزع القطع على الأطباق في كل طبق 3 قطع
3- أعد المجموعات التي بها عدد متساوي من المجموعات، أجد أنها 4 مجموعات متساوية وهناك مجموعة تحتوي فقط على قطعة واحدة، إذا لا يمكن توزيع 13 على مجموعات متساوية مكونة من 3 قطع
علاقة القسمة بالطرح
أستعد: تحوي علبة 15 قلماً بألوان مختلفة، حمراء، و زرقاء و صفراء و بأعداد متساوية، فما عدد الأقلام من كل لون؟
عندما أقسم فإنني أوزع عدداً من القطع في مجموعات متساوية، لأجد عدد تلك المجموعات أو عدد القطع في كل مجموعة
تمرين: وزعت 16 وردة في زهريات، فوضعت 4 وردات في كل مزهرية، فما عدد الزهريات؟
استعمل 16 وردة و أقسمهم إلى مجموعات في كل مجموعة 4 وردات؛ ثم نعد عدد المجموعات نجد أنها ؛ مجموعات الجملة العددية: 16 ÷ 4 = 4
أتحدث: مبيناً كيف أستعمل خط الأعداد لأجد ناتج القسمة 18 ÷ 9
استعمال خط الأعداد لإيجاد 18 ÷ 9
أبدأ من العدد 18 و أقفز 9 وحدات باتجاه الصفرء ثم 9 وحدات أخرى حتى أصل إلى العدد صفرء ثم أعد القفزات فيكون عددها هو الناتج
تمرين: قطعت ربة منزل كل برتقالة 8 شرائح، و وضعتها جميعاً في طبق واحد إذا كان في الطبق 16 شريحة، فما عدد البرتقالات التي قطعتها؟
بما أن عدد الشرائح في الطبق 16 شريحة، كل برتقالة تقطع إلى 8 شرائح
الخطوة 1: أحضر 16 شريحة من البرتقال وأطباق تستعمل كمجموعات
الخطوة 2: أوزع الشرائح على الأطباق بالتساوي في كل طبق 8 شرائح
الخطوة 3:
أعد المجموعات التي بها عدد متساوي من الشرائح؛ نجد أنهم مجموعتان
الصيغة العددية
إذاً عدد البرتقال 16 ÷ 8 = 2 برتقالة
تمرين: طريق طوله 16 كيلو متراً، تم تقسيم العمل فيه إلى مراجل طول كل مرحلة منها 2 كيلو متر، فما عدد المراحل؟
بما أن طول الطريق 16 كيلومتر؛ وطول كل مرحلة 2 كيلو متر، نقسم المسافة الكلية على طول المرحلة لنحصل على عدد المراحل
الخطوة 1: أحضر 16 قطعة تعبر عن المسافة؛ أطباق تعبر عن المجموعات
الخطوة 2: أوزع القطع على الأطباق بالتساوي ليكون في كل طبق قطعتين
الخطوة 3: أعد المجموعات المتساوية في العدد؛ نجد أنها 8 مجموعات
الصيغة العددية 16 ÷ 2 = 8 مراحل
فصل القسمة (2)
تمرين: يلعب فهد و سمير مع 3 أصدقائهما، فإذا كان معهما 45 كرة زجاجية، فهل يمكن توزيعها عليهم بالتساوي؟ أوضح إجابتي
عدد الأشخاص = 5 + 2 = 7
عدد الكرات لكل الأشخاص = عدد الكرات ÷ عدد الأصدقاء
= 49 ÷ 7 = 7 كرات
نعم، يمكن توزيعها عليهم بالتساوي
تمرين: لماذا أستعمل الشبكات لأجد ناتج القسمة؟
استعمل الشبكات لإيجاد ناتج القسمة لإمكانية تقسيمها حسب المسائل لمعرفة الناتج
اكتب: كيف أستعمل الشبكات لأجد ناتج القسمة.
استعمل الشبكات لمعرفة ناتج القسمة بجعل المقسوم عدد كلي و المقسوم عليه عدد مجموعات متساوية و العدد الذي تحتوي عليه كل مجموعة يكون هو ناتج القسمة
أتحدث: أشرح كيف أستعمل حقائق الضرب و القسمة المترابطة لأجد ناتج القسمة
لأن عملية الضرب أو القسمة تتكون كل منها من 3 أعداد مترابطة تشكل 3 حقائق مترابطة و أنهما عمليتان متعاكستان؛ فإنه من المقيد معرقة أحد هذه الحقائق لتعرف الحقائق الأخرى
تمرين: في أيام الاثنين و الأربعاء و الجمعة، ركض محمود 3 كلم، و في باقي أيام الأسبوع ركض 2 كلم، ما عدا يوم السبت كان يوم راحة، و ركض يوم الأحد ضعف ما ركضه يوم الاثنين، فكم كيلو متراً ركض محمود خلال الأسبوع كله؟
يوم الاثنين والأربعاء والجمعة ركض 3 كلم
باقي الأيام (الثلاثاء و الخميس) ركض 2 كلم ما عدا السبت يوم الأحد ركض 2 × 1 = 2 كلم
إذن ركض محمود 2 + 2 + 3 = 7 كلم
تمرين: تضم حافة صفين طولين من المقاعد في كل صف 20 مقعداً، فكم حافلة من النوع نفسه نحتاج لتوفير 200 مقعد؟
الحافلة تحتوي على صفين و كل صف فيه 20 مقعد إذن الحافلة الواحدة تحتوي على 20 + 20 = 40 مقعد، إذن عدد الحافلات = 200 ÷ 40 = 5 حافلات
فصل القياس
تمرين: أيهما أدق، القياس بالملمترات أم السنتمترات؟ أضوح إجابتي مستفيداً من الشرح
القياس بالمليمترات أدق حيث أن السنتمتر الواحد مقسم إلي ١٠ أقسام كل منها يسمى مليمتراً؛ و بعض الأشياء يكون طولها أكبر قليلاً من السنتمتر
أتحدث: أشرح كيف أختار الوحدة المناسبة لقياس طول شيء ما.
أستعمل الملتمر و السنتمتر لقياس الأطوال الصغيرة؛ و المتر للأطوال الكبيرة؛ و الكيلو متر للمسافات الطويلة
تمرين: اشترك عدد من العمال في زراعة حديقة أحد المنازل، فعمل كل منهم 4 ساعات يومياً، و لمدة يومين، إذا كان مجموع ساعات العمل لهم جميعاً هو 24 ساعة، فكم عاملاً شارك في زراعة الحديقة؟
كل عامل عمل ساعات في اليوم، إذا في اليومين ساعات العمل 8 ساعات لكل عامل و بما أن مجموع ساعات العمل للجميع = 24، إذا عدد العمال = 24 ÷ 8 = 3 عمال
أكتب: أشرح كيف يمكن لشيئين مختلفين في الشكل و الأبعاد أن يكون لهما الحجم نفسه
يمكن أن يكون لشيئين مختلفين الحجم نفسه إذا كان في كل منهما العدد نفسه من المكعبات؛ و لكن ترتيب المكعبات فيهما مختلف
أكتب: ما الفرق بين المساحة و الحجم؟
المساحة هي عدد الوحدات المربعة اللازمة لتغطية شكل ثنائى الأبعاد من غير تداخل؛ بينما الحجم عدد الوحدات المكعبة اللازمة لملء حيز يشغله شكل ثلاثي الأبعاد
فصل الأشكال الهندسية
أتحدث: ما أوجه الاختلاف و الشبه بين المخروط و الأسطوانة؟
أوجه الشبه: كلاهما مجسمات أما المخروط له وجه دائري واحد
أكتب: ما الخصائص المشتركة بين المكعب و متوازي المستطيلات؟
الخصائص المشتركة هي عدد الأوجه: 6، عدد الأحرف: 12، عدد الرؤوس في كل منهما: 8، و كل منهما مجسم
أتحدث: أشرح لماذا لا يكون شكل الطبق مضلعاً
يتكون المضلع من قطع مستقيمة و الطبق المرسوم ليس له اضلاع
تمرين: هل الشكل المجاور يعد مضلعاً؟ أوضح إجابتي
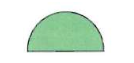
لا؛ لأن المضلع يتكون من قطع مستقيمة و هذا الشكل لا يحتوي علي قطع مستقيمة
توضيح الإجابة: لأنه على شكل نصف دائرة
أكتب: ما أوجه الاختلاف بين الشكل السداسي و الشكل الثماني؟
الشكل السداسي: مضلع مكون من 6 أضلاع و له 6 زوايا
الشكل الثماني: مضلع مكون من 8 أضلاع و له 8 زوايا
تمرين: مجسمان مجموع أوجههما 3 أوجه، و لكل منهما ضلع منحن، أسمي المجسمين، ثم أكتب الخطوات التي سأستعملها لحل المسألة
المجسمان هما المخروط و الأسطوانة
أفهم: ماذا أعرف من المسألة؟
مجسمان لهم 3 أوجه لكل منها ضلع منحني، ما المطلوب؟
أسمي المجسمين
خطط: أحل مسألة أيسط كي أاجد اسم المجسمين
حل: المجسم الذي له وجهان و له ضلع منحني هو الأسطوانة، إذن يتبقى وجه واحد و المجسم الذى له وجه واحد هو المخروط
تحقق: أراجع الحل؛ الجواب يتفق مع الحقائق المعطاة في المسألة
إذن الجواب صحيح
اكتب: اشرح متى أستعمل خطة (حل مسألة أبسط) في الحل
عندما تكون المسألة صعبة لا أقدر على حلها فأستعمل خطة حل مسألة أبسط لمعرفة الحل
اكتب: هل يمكن لشكل ما أكثر من محور تماثل؟ أوضح إجابتي
نعم، توضيح الإجابة: عند طي الشكل بأكثر من طريقة و نجد في كل مرة أن النصفين متماثلين
فصل عرض البيانات و تفسيرها
تحدث: كيف يساعدني الجمع المتكرر في تفسير التمثيل بالرموز؟
كل صورة رمزية تمثل عدداً، أستعمل الجمع المتكرر عدداً من المرات يقّدر عدد الصور الرمزية التي أريد أن أجد عدد الأشياء أو الأشخاص التي تمثلها
حلل الخطة:
بكم طريقة يمكن لمحمد و ياسر و مهند أن يصطفوا لكي يدخلوا غرفة الصف؟ أجيب عن الأسئلة التالية:
1- أشرح لماذا كانت خطة إنشاء قائمة مفيدة في حل هذه المسألة
خطة إنشاء قائمة مفيدة فى معرفة الطرق المختلفة لترتيب الطلاب لأنها تبين الترتيبات جميعها دون تكرار
2- أشرح كيف أنظم الترتيبات المختلفة جميعها في جدول
ابدأ بمفردة و اربطها بالمفردات الأخرى جميعها، ثم اكرر ذلك من باقي المفردات
تكوين جدول يتكون من 6 صفوف و 3 أعمدة و كتايبة أسماء الطلاب بداخله
3- إذا كان عدد الطلاب 4، فما عد الطرائق المختلفة لاصطفافهم؟
عدد الطرق المختلفة لاصطفافهم = 24 طريقة
4- كيف أعرف أن إجابتي عن السؤال السابق صحيحة؟
أنظمها في جدول و أتأكد من العدد؛ تكون صحيحة إذا لم تتكرر أي من طرق الترتيب
اكتب: ما أهمية كتابة العنوان و المسميات في التمثيل بالرموز؟
لتوضيح البيانات و سهولة التعامل معها
فكر:
1- كيف أحدد التدريج الذي سأستعمله؟
على أساس عدد الإشارات الموجودة في المسألة
2- لماذا جعلت التدريج هو مضاعفات العدد 2؟
حتى يكون آخر رقم هو 12 فتكفي اللوحة لتمثيل كل الإشارات
3- لماذا تنتهي بعض الأعمدة بين عددين أو بين سطرين؟
لأن التدريج هو مضاعفات العدد 2 و بعض الإشارات تكون عدد فردي فلا بد أن تكون بين عددين زوجين
فصل الكسور
اكتب: أشرح كيف أمثل الكسر 1/16 بنموذج
أطوي ورقة من المنتصف أربع مرات فاحصل على 16 جزءاً متطابقاً؛ ثم أفتحها لأرى أن كل جزء منها يمثل ب الورقة
أتحدث: أوضح كيف أستعمل الكسر لأعبر عن الجزء المظلل من شكل مقسم إلى أجزاء متطابقة
لكي أعبر عن الجزء المظلل من شكل مقسم إلى أجزاء متطابقة، أكتب عدد الأجزاء المظللة فى بسط كسر؛ و عدد أجزاء الشكل كلها فى مقامه
أكتب: أشرح كيف أكتب كسراً يمثل جزءاً من كلّ
أعد الأجزاء المتطابقة جميعها و أضع الناتج في المقام؛ ثم أعد الأجزاء المتطابقة التي تصف الكسر و أضع الناتج في البسط
تمرين: يوجد 7 بطاقات ملونة في حقيبة، إذا كان 6 بطاقات منها زرقاء، و بطاقة واحدة منها حمراء، أصف احتمال اختيار بطاقة زرقاء؟
الاحتمال الأكثر أن تكون زرقاء
أكتب: كيف أعرف إذا كان الكسران متكافئين أم لا؟
إذا مثل الكسرين الكمية نفسها؛ أو النموذج نفسه؛ فإنهما يكونان متكافئين، و إذا لم يكونا كذلك، فإنهما لا يكونان متكافئين
تمرين: لدى تركي 7 مجموعات من أوراق الملاحظات اللاصقة، خمس منها ذات لون وردي، و واحدة خضراء، و واحدة زرقاء، أكتب الكسر الذي يبين مجموعات الأوراق غير الوردية؟
المجموعات غير الوردية = 2/7
حلل الخطة:
جمع أحمد و أخوه 8 وردات، ثم وضعها في زهرية، فإذا كان نصف الوردات حمراء و واحدة صفراء و الباقي بيضاء، فما عدد الوردات البيضاء؟ أجيب عن الأسئلة التالية:
1- أفسر لماذا قسمت الشكل إلى 8 أجزاء متطابقة
لأنه توجد 8 وردات
2- أشرح لماذا لونت 4 أجزاء من 8 أجزاء باللون الأحمر
لتمثل عدد الوردات الحمراء
3- أفترض أن لدى أحمد و أخيه 10 وردات، فكم سيكون عدد الوردات البيضاء؟
سيكون عدد الوردات البيضاء = 4
مسألة مفتوحة: أكتب مسألة من واقع الحياة يحتاج حلها إلى مقارنة كسرين
قسمت فاطمة فطيرتين من الحجم نفسه، إذا أخذت أختها ¾ من الفطيرة الأولى، و أخذت فاطمة 4/6 من الفطيرة الثانية، فهل أخذت كلتاهما الحجم نفسه؟
تدرب على الخطة:
تقاسم عصام و عدنان و ياسر 12 كتاباً، فأخذ عصام ⅓ الكتب، و أخذ عدنان كتابين في حين أخذ ياسر الكتب الباقية، فما عدد الكتب التي أخذها ياسر؟
أفهم:
معطيات: تقاسم عصام و عدنان و ياسر 12 كتاباً، فأخذ عصام ⅓ الكتب، و أخذ عدنان كتابين في حين أخذ ياسر الكتب الباقية
المطلوب: ما عدد الكتب التي أخذها ياسر؟
خطط: ارسم صورة لأجد حل المسألة
حل: عدد الكتب التي أخذها عصام =4 كتب باللون الأخضر
عدد الكتب التي أخذها عدنان =2 كتاب ياللون الأزرق
عدد الكتب التي أخذها ياسر =6 كتب باللون الأحمر
تحقق: تحقق من الرسم، إذن الإجابة صحيحة




