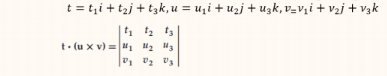ملخص الفصل الأول المتجهات رياضيات 6 مقررات
مقدمة في المتجهات
الكميات القياسية و الكميات المتجهة :
كمية قياسية ( عددية ) :
هي التي تتحدد بالمقدار و الوحدة فقط مثل : الطول و الزمن
كمية متجهة :
الكميات المتجهة هي التي تتحدد بالمقدار و الاتجاه و نقطة التأثير مثل : الوزن ( الثقل ) - القوة - السرعة - العجلة
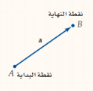
مكن تمثيل المتجه هندسيا بقطعة مستقيمة لها اتجاه ( قطعة مستقيمة متجهة ) أو سهم يظهر كلا من المقدار و الاتجاه . و يمثل الشكل المجاور القطعة المستقيمة المتجهة التي لها نفطقة البداية A و نقطة النهاية B و يرمز لهذا المتجه بالرمز AB
أما طول المتجه : فهو عبارة عن طول القطعة المستقيمة التي نمثله غغي الشكل المجاور إذا كان مقياس الرسم هو 1سم
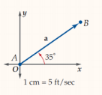
يكون المتجه في الوضع القياسي . إذا كانت نقطة بداية المتجه هي نقطة الاصل و يعبر عن اتجاه المتجه بالزاوية التي يصنعها مع الاتجاه الافقي ( الاتجاه الموجب للمحورX ) فمثلا : اتجاه المتجه a هو 35
ويمكن التعبير عن اتجاه المتجه ايضا باستعمال زاوية الاتجاه الربعي وقرأ فاي وهي زاوية قياسها 0 و 90 شرق أو غرب الخط الرأسي ( خط شمال - جنوب )
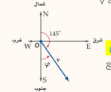
فمثلا زاوية الاتجاه الربعي للمتجه V في الشكل المجاور هي 35 جنوب شرق
كما يمكن استعمال زاوية الاتجاه الحقيقي حيث نقاس الزاوية مع عقارب الساعة بدءا من الشمال و يقاس الاتجاه الحقيقي بثلاثة أرقام فمثلا يكتب الاتجاه الذي يحدد زاوية قياسها 25 من الشمال مع عقارب الساعة باستعمال الاتجاه الحقيقي على الصورة 025
قاعدة المثلث
لإيجاد محصلة المتجهين a.b اتبع الخطوات الآتية
الخطوة الاولى : أجر انسحابا للمتجهة b بحيث تلتقي نقطة بدايته مع نقطة نهاية المتجهة a
الخطوة الثانية : محصلة المتجهين a ، b هي المتجهة المرسوم من نقطة بداية a إلى نقطة نهاية b
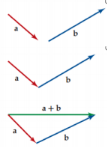
قاعدة متوازي الأضلاع
لإيجاد محصلة المتجهين a ، b ابتع خطوات الآتية
الخطوة الاولى : أجر انسحابا للمتجهة b بحيث تلتقي نقطة بدايته مع نقطة نهاية المتجهة a
الخطوة الثانية : أكمل رسم متوازي الاضلاع الذي ضلعاه a ، b
الخطوة الثالثة : محصلة المتجهين هي تلك المتجهة الذي يمثله قطر متوازي الاضلاع
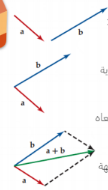
عند جمع متجهين متعاكسين لهما الطول نفسه ، فإن المحصلة هي المتجه الصفري
ويركز له بالرمز 0 و طوله صفر و ليس له اتجاه . و عملية طرح المتجهات تشبه عمليه طرح الاعداد . لإيجاد p-q اجمع المعكوس q
إلى : أي أن pp+(-q)=p-q
و كذلك يمكن ضرب المتجه في عدد حقيقي إذا ضرب المتجه v في عدد حقيقي k فإن طول المتجه kv هو /k//v و يتحدد بإشارة k
إذا كانت k>0 فإن اتجاه kv هو اتجاه v نفسه إذا كانت k<0 فإن اتجاه kv هو عكس اتجاه v
المتجهات في المستوى الإحداثي
مفهوم أساسي
الصورة الاحداثية لمتجه :
الصورة الإحداثية AB
الذي نقطة بدائية A( X1.Y1) و نقطة نهايته B( X2.Y2) هي :
(X2-X1.Y2-Y1)
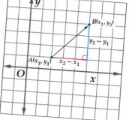
مفهوم أساسي
طول المتجه في المستوى الإحداثي :
إذا كان v متجها نقطة بدائية ( X1.Y1) و نقطة ( X2.Y2)
فإن طول v يعطى بالصيغة
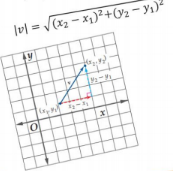
جمع متجهين
a+b(a1+b1.a2+b2)
طرح متجهين
a - b(a1 - b1.a2 - b2)
العمليات على المتجهات
ضرب متجه في عدد حقيقي Ka=( ka1.ka2)
تشبه عمليات الضرب في عدد حقيقي و الجمع و الطرح على المتجهات العمليات نفسها على المصفوفات
مفهوم أساسي
الضرب الداخلي لمتجهين في المستوى الإحداثي
يعرف الضرب الداخلي للمتجهين
a=(a1.a2). b (b1.b2)
a × b=a1 b1+a2 b2
مفهوم أساسي
المتجهان المتعامدان
يكون المتجهان غير الصفريين a.b متعامدين فقط إذا كان0 =a × b
الخاصية الإبدالية
u × v= u × v
خاصية التوزيع
u × (v+w)
u × v+u × w
خاصية الضرب في عدد حقيقي
K(U ×V)=Ku× v
u × Kv
خاصية الضرب الداخلي و طول المتجه
U ×U=U2
نظرية
خصائص الضرب الداخلي :
إذا كانت v. u . w متجهات وكان Kعددا حقيقيا فإن الخصائص الآتية صحيحة
المتجهات في الفضاء الثلاثي الابعاد
هو نظام إحداثس الابعاد يتشكل بواسطة خطي أعداد متعامدين هما المحور x و المحور y اللذان يتقاطعان في نقطة تسمى نقطة الاصل و يسمح لك هذا النظام بتحديد وتعيين نقاط في المستوى و تحتاج إلى نظام الإحداثيات الثلاثي الابعاد لتعيين نقطة في الفضاء مبدأ بالمستوى xy و نضعه بصورة تظهر للشكل ثم نضيف محورا ثالثا يسمى المحور z يمر بنقطة الاصل و يعامد كلا من المحورين y.x فيكون لدينا ثلاثة مستويات هي xy.zy.xz و تقسم هذه المستويات الفضاء إلى ثماني مناطق
مفهوم أساسي
صيغتا المسافة و نقطة المنتصف في الفضاء
تعطي المسافة بين النقطتين

مفهوم أساسي
العمليات على المتجهات في الفضاء
جمع متجهين
a+b=(a1+b1.a2+b2.a3+b3)
طرح متجهين
a - b=(a1 - b1.a2 - b2.a3 - b3)
ضرب منجه في عدد حقيقي
Ka=(Ka1.Ka2.Ka3 )
مفهوم أساسي
الضرب الداخلي و المتجهات المتعامدة في الفضاء
يعرف الضرب الداخلي للمتجهين
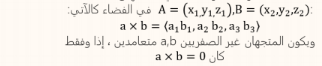
مفهوم أساسي
الضرب القياسي الثلاثي