حل درس حل نظام من معادلتين خطيتين رياضيات ثالث متوسط
السؤال : استعمل الحاسبة البيانية لحل كل من أنظمة المعادلات الآتية و قرب الحل إذا كان كسرا عشريا إلى أقرب جزء من مئة
ص = 2س - 3
ص = -4.0 س + 5
الجواب :
الخطوة الاولى : المعادلات محلولة بالنسبة للمتغير ص
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
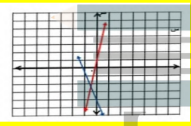
اكتب المعادلة الاولى ص = 2س - 3 ثم اضغط المفتاح enter فيظهر التمثيل البياني
اضغط menu و اختر منها point and line ومنها اختر intersection point وقم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع ( 3.3 ، 3.7 ) التي هي حل النظام
ص = 6س + 1
ص = -2.3 س - 4
الجواب :
الخطوة الاولى : المعادلات محلولة بالنسبة للمتغير ص
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
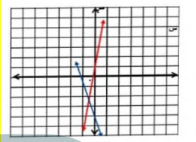
اكتب المعادلة الاولى ص = 6س +1
ثم اضغط المفتاح enter فيظهر التمثيل البياني
اضغط المفتاح tab ثم اكتب المعادلة الثانية
ص = -2.3 س - 4 ثم اضغط enter لظهر التمثيل البياني
اضغط menu و اختر منها point and line ومنها اختر intersection point وقم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع (-0.54 ، -2.26) التي هي حل النظام
ص = 6س + 1
عند س = 0 ص = 1 النقطة ( 1.0 )
ص = 0 ص = 1 النقطة ( 1.0 )
ص = 0 س = -0.16 النقطة ( 0.016- )
ص = -2.3 س - 4
عند س = 0 ص = -4 النقطة ( 0.-4 )
عند ص = 0 س = 1.25- النقطة ( 0 ، 1.25- )
7س - 2 ص = 16
11س + 6ص = 32.3
الجواب :
الخطوة الاولى : حل المعادلات بالنسبة للمتغير ص
7س - 2 ص= 16
7س - 7س -2ص = 16 -7 س
-2ص = 16-7س
ص = -8 + 3.5 س ( 1 )
11س + 6ص = 32.3
11س -11س + 6 ص = 32.3 -11 س
6ص = 32.3 - 11 س
ص = 5.4 -1.8 ( 2 )
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
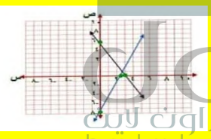
اكتب المعادلة الاولى ص = 3.54 س - 8
ثم اضغط المفتاح enter فيظهر التمثيل البياني
اضغط المفتاح tab ثم اكتب المعادلة الثانية
ص = 1.8 -5.4 س ثم اضغط enter لظهر التمثيل البياني
اضغط menu و اختر منها point and line ومنها اختر intersection point وقم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع (2.51 ، 0.78 ) التي هي حل النظام
ص = -8 +3.5 س
عند س = 0 ص = -8 النقطة ( 0 ، -8 )
ص = 0 س = 2.3 النقطة ( 2.3 ، 0 )
ص = 5.4 - 1.8 س
عند س = 0 ص 5.4 النقطة ( 0 ، 5.4 )
عند ص = 0 س = 3 النقطة ( 0.3 )
3 س + 2ص = 16
5س + ص = 9
الجواب :
الخطوة الاولى : حل المعادلات بالنسبة للمتغير ص
3س + 2ص = 12
3س - س + 2ص = 16 -3س
2ص = -3س + 16
ص = -1.5 س + 8 ( 1 )
5س + ص = 9
ص = -5س +9 ( 2 )
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
اكتب المعادلة الاولى ص = -1.5 س + 8
ثم اضغط المفتاح enter فيظهر التمثيل البياني
اضغط المفتاح tab ثم اكتب المعادلة الثانية
ص = -5س +9 ثم اضغط enter لظهر التمثيل البياني
اضغط menu و اختر منها point and line ومنها اختر intersection point وقم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع (0.29 ، 7.57 ) التي هي حل النظام
62.0 س + 0.35 ص = 1.60
-1.38 س + ص = 8.24
الجواب :
الخطوة الاولى : حل المعادلات بالنسبة للمتغير ص
0.62 س + 0.35 ص = 1.60
0.62 س - 0.62 س + 0.35 ص = 1.60 - 0.62 س
0.35 ص = 1.60 -0.62 س
ص = 4.6 - 1.8 س ( 1 )
-1.38 س + ص = 8.24
-1.38 س + 1.38 س + ص = 8.24 + 1.38 س
ص = 8.24 +1.38 س ( 2 )
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
اكتب المعادلة الاولى ص = 4.6 -1.8 س
ثم اضغط المفتاح enter فيظهر التمثيل البياني
اضغط المفتاح tab ثم اكتب المعادلة الثانية
ص = 8.24 + 1.38 س ثم اضغط enter لظهر التمثيل البياني
اضغط menu و اختر منها point and line ومنها اختر intersection point وقم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع ( -16.1 ، 6.63) التي هي حل النظام
75س - 100 ص = 400
33س -10 ص = 70
الجواب :
الخطوة الاولى : حل المعادلات بالنسبة للمتغير ص
75 س - 100 ص = 400
100ص = 75 س - 400
ص = 0.75 - 4 ( 1 )
33 س - 10 ص = 70
10ص = 33س - 70
ص = 3.3 س -7 ( 2 )
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
اكتب المعادلة الاولى ص = 0.75 - 4
ثم اضغط المفتاح enter فيظهر التمثيل البياني
اضغط المفتاح tab ثم اكتب المعادلة الثانية
ص = 3.3 س - 7 ثم اضغط enter لظهر التمثيل البياني
اضغط menu و اختر منها point and line ومنها اختر intersection point وقم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع ( 1.18 ، -3.12) التي هي حل النظام
السؤال : استعمل الآلة الحاسبة البيانية لحل كل من المعادلات الآتية، وقرب الحل إذا كان كسراً عشرياً إلى أقرب جزء من مئة:
4س -2 = -6
الجواب :
الخطوة الاولى : اكتب نظام من معادلتين على ان يساوي كل طرف من طرفي المعادلة ص
ص = 4س -2 ص = -6
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
اكتب المعادلة الاولى ص = 4س - 2
ثم اضغط المفتاح enter فيظهر التمثيل البياني
اضغط المفتاح tab ثم اكتب المعادلة الثانية
ص = -6 ثم اضغط enter لظهر التمثيل البياني
حدد نقطة التقاطع مستعملا المفاتيح التالية : menu ، point and line ، intersection point ثم قم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع و يكون الحل -1
3 = 1 - س/2
الجواب :
الخطوة الاولى : اكتب نظام من معادلتين على ان يساوي كل طرف من طرفي المعادلة ص
ص = 1 + س/2 ، ص = 3
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
اكتب المعادلة الاولى و ادخل المعادلة الثانية
ثم اضغط المفتاح enter فيظهر التمثيل البياني
حدد نقطة التقاطع مستعملا المفاتيح التالية : menu ، point and line ، intersection point ثم قم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع و يكون الحل 4
-2 + 10 س = 8س -1
الجواب :
الخطوة الاولى : اكتب نظام من معادلتين على ان يساوي كل طرف من طرفي المعادلة ص
ص =-2 +10س ، ص =8س - 1
الخطوة الثانية : مثل كلا من المعادلتين بيانيا لإيجاد الحل
أفتح الالة الاسبة بالضغط على on ثم اختر new documeny
اختر add graphs فتظهر شاشة
اكتب المعادلة الاولى و ادخل المعادلة الثانية
ثم اضغط المفتاح enter فيظهر التمثيل البياني
حدد نقطة التقاطع مستعملا المفاتيح التالية : menu ، point and line ، intersection point ثم قم بالضغط على المستقيم الاول ثم المستقيم الثاني فتظهر نقطة التقاطع و يكون الحل0.5
السؤال : اكتب : وضح لماذا يمكنك حل معادلة مثل ر = أس + ب بحل نظام العادلتين ص = ر ، ص = أ س + ب
الجواب :
عند تقاطع التمثيلان المتباينان ص = 1
ص = أ س + ب تكون قيم ص متساوية و عندها تكون ر = أس + ب



