حل درس نظام من معادلتين خطيتين بالحذف باستعمال الضرب رياضيات ثالث متوسط

حل درس نظام من معادلتين خطيتين بالحذف باستعمال الضرب رياضيات ثالث متوسط

السؤال : تحقق من فهمك

6س - 2ص = 10

3س - 7ص = -19

الجواب : 

اضرب المعادلة الثانية في -2 

-6 س  + 14 ص = 38 

6س - 2ص = 10 

ــــــــــــــــــــــــــــــــــ

12ص = 48

ص = 4

عوض عن ص في إحدى المعادلات 

6س - 2 ( 4 ) = 10

6س - 8 = 10

6س = 18

س = 3

الحل : ( 4،3 ) 

9 ر + ك = 13

3ر + 2ك = -4 

الجواب : 

اضرب المعادلة الثانية في -3 

 -9 ر -6 ك = 12

9 ر + ك = 13 

ــــــــــــــــــــــــــــــ

-5 ك = 25

ك = -5

عوض عن ك في إحدى المعادلات 

9 ر + ( -5 ) = 13

9 ر = 18

ر = 2 

الحل ( -5، 2 )

السؤال : تحقق من فهمك

5س - 3ص = 6

2س +5ص = -10 

الجواب :

اضرب المعادلة الاولى في 2 و الثانية في 5 

 10 س - 6ص = 12

10 س + 25 ص = 50    أطرح المعادلتين

ــــــــــــــــــــــــــــــــــــــــــــــ

-31 ص = 62 

 ص = -2 

عوض عن ص في إحدى المعادلات 

5س - 3 ( -2 ) = 6

5س = 0

س = 0 

 الحل : ( 0، -2 ) 

 6 أ + 2 ب= 2

4 أ + 3 ب = 8

الجواب :

اضرب المعادلة الاولى في 3 و الثانية في 2

18 أ + 6 ب = 6

8 أ + 6 ب = 16 اطرح المعادلتين 

______________
10 أ = -10 

عوض عن أ في إحدى المعادلات

6 ( -1 ) + 2 ب = 2

2ب = 8

ب = 4

الحل : ( -1، 4 ) 

السؤال : زورق: يقطع زورق 4 أميال في الساعة في اتجاه التيار ، ويستغرق في رحلة العودة 1,5 ساعة، أوجد معدل سرعة القارب في المياه الساكنة.

الجواب : 

افترض ان س معدل سرعة الزورق ، ص سرعة التيار 

س + ص = 4 ـــــــــــــــــ 1.5 س + 1.5 ص = 6

( س - ص ) 1.5 = 4 ـــــــــــــــــ 1.5 س -1.5 ص = 4

3س = 10    س = 3.3 

معدل سعة الزورق = 3.3 ميل / ساعة

السؤال :حل كلا من أنظمة المعادلات الآتية مستعملاً الحذف:

2س - ص = 4

7س + 3ص = 27 

الجواب : 

اضرب المعادلة الاولى في 3 

6س -3ص = 12

7س +3ص = 27  اجمع المعادلتين 

_______________

13 س= 39 

س = 3 

 عوض عن س في إحدى المعادلات 

2 ( 3 ) - ص = 4

ص = 2 
 

2س + 7ص = 1

س + 5ص = 2 

الجواب : 

اضرب المعادلة الثانية في 2 

 2س + 10 ص = 4

2س +7ص   اطرح المعادلتين 

____________

3ص = 3 

 ص = 1

عوض عن ص في إحدى المعادلات 

2س + 7 ( 1 ) = 1

2س = -6 

س = -3 

الحل ( -3 ، 1 ) 

4س + 2ص = -14 

5س +3ص = -17

الجواب : 

اضرب المعادلتين الاولى في 3 و الثانية في 2

12 س +6 ص= -42ى 

10+6ص = 34 س   اطرح المعادلتين 

____________

2س = -8 

 س= -4 

 عوض عن س في إحدى المعادلات 

4 ( -4 ) + 2 ص = -14

2ص = 2 

ص = 1 

الحل (  -4 ، 1 )

السؤال : صيد: يقطع قارب صيد مسافة 10 أميال في 30 دقيقة في اتجاه مجرى النهر، إلا أنه يقطع المسافة نفسها في رحلة العودة في 40 دقيقة ، أوجد معدل سرعته في المياه الساكنة بوحدة ميل/ساعة.

الجواب : 

افترض ان س سرعة القارب ، ص سرعة النهر 

( س+ ص) 30 = 10        30+30 ص = 10

( س - ص ) 40 = 10       40 س - 40 ص = 10

اضرب المعادلة الاولى في 4 و الثانية في 3

120 س +120 ص = 40

120 س - 120 ص = 30

240 س = 70

س = 0.291 

معدل سرعة القارب 0.291 × 60 = 17.5 ميل / ساعة

السؤال : حل كلا من أنظمة المعادلات الآتية مستعملاً طريقة الحذف: 

س + ص = 2

-3س +4ص = 15

الجواب : 

اضرب المعادلة الاولى في 3

3س +3ص = 6 

-3س +4ص = 15    اجمع المعادلتين 

______________

7ص = 21 

 ص = 3 

 عوض عن ص في إحدى المعادلات 

 س+3 = 2 

 س = -1 

 الحل : ( -1، 3 ) 

س -ص = -8 

7س + 5ص = 16

الجواب : 

اضرب المعادلة الاولى في 5 

5س - 5ص = -40 

7س + 5ص = 16 اجمع المعادلتين

_____________

12 س= -24 

س= -2 

عوض عن س في إحدى المعادلات

-2-ص = -8 

= 6

6س + ص = -39

3س +2ص = -15

الجواب : 

اضرب المعادلة الاولى في

12س  + 2ص = -78

3س +2ص = -15   اطرح المعادلتين 

____________

9س = -63 

س = -7

عوض عن س في إحدى المعادلات 

6 ( -7 ) + ص = 39-

ص = 3

الحل : ( -7 ، 3 )

2س + 5 ص = 11

4س +3ص = 1

الجواب : 

اضرب المعادلة الاولى في 2

4س + 10 ص= 22

4س + 3ص = 1   أطرح المعادلتين

______________

7ص = 21

ص = 3

عوض عن ص في إحدى المعادلات 

2س +5( 3 ) = 11

2س = -4

س = -2 

الحل : ( -2 ، 3 )

3س + 4ص = 29

6س +5ص = 43

الجواب : 

اضرب المعادلة الاولى في 6 و المعادلة الثانية في 3

18 س + 24 ص = 14

18 س+15 ص = 129  اطرح المعادلتين 

_______________

9ص = 45

ص = 5

عوض عن ص في إحدى المعادلتين 

3س + 4 ( 5 ) = 29

3س = 9

س = 3 

 الحل : ( 3 ، 5 ) 

4س + 7ص = -80

3س + 5ص = -58

الجواب : 

اضرب المعادلة الاولى في 3 و المعادلة الثانية في 4

12س +21 ص = -240 

12 س +20ص =  - 232 اطرح المعادلتين

___________

ص = -8 

عوض عن ص في إحدى المعادلات 

4س + 7 ( -8 ) = -80 

4س = -24 

س = -6

الحل : ( -6 ، -8 ) 

12س -3ص = -3 

6س +ص = 1

الجواب : 

اضرب المعادلة الثانية في 3 

12 س - 3ص = -3

18 س + 3 ص= 3  اجمع المعادلتين  

_______________

30 س = 0 

س =0

عوض عن س في إحدى المعادلات 

ص = 1 

 الحل : ( 1،0 ) 

-4 س+ 2ص = 0

10 س +3ص = 8

الجواب :

اضرب المعادلة الاولى في 10 و المعادلة الثانية في 4 

-40 س + 20 ص = 0 

40س + 12 ص = 32   اجمع المعادلتين 

________________

32 ص = 32 

ص = 1 

عوض عن ص في إحدى المعادلات 

-4س + 2 ( 1 ) = 0

-4 س = -2 

س = 0.5

السؤال : نظرية الأعداد: ما العددان اللذان سبعة أمثال أحدهما زائد ثلاثة أمثال الآخر يساوي سالب واحد، ومجموعهما يساوي سالب ثلاثة؟

الجواب : 

افترض العددان س ، ص 

7س + 3ص = -1      7س + 3ص = -1

س +ص = -3    × 3    3س + 3ص = -9

_____________

4س = 8 

س = 2

عوض عن س في إحدى المعادلات 

2+ص = -3 

 ص = -5 

الحل 

( 2 ، 5- ) 

السؤال : كرة قدم: سجل أحد لاعبي كرة القدم (12) هدفاً في الدوري الممتاز. فإذا علمت أن ضعف عدد الأهداف التي سجلها في مرحلة الذهاب تزيد على ثلاثة أمثال أهدافه في مرحلة الإياب بـ 4 ، فما عدد أهدافه في كل من مرحلتي الذهاب والإياب؟

الجواب : 

عدد أهداف الذهاب س و عدد أهداف الإياب ص 

س + ص= 12 × 3        3س + 3ص = 36 

2س - 3ص = 4          2س - 3 ص = 4

                               __________  

 5س = 40 

س= 8

عوض عنس في إحدى المعادلات 

8+ص = 12

ص = 4

عدد أهداف الذهاب = 8 اهداف 

عدد اهداف الإياب = 4 أهداف

السؤال : حل كلا من أنظمة المعادلات الآتية مستعملاً طريقة الحذف:

-0.4 س + 0.25 ص = -2،175

2س +ص = 7،5

الجواب : 

بقسمة المعادلة الاولى على 0.25 

-1.6 س + ص = -8.7

2س +ص = 7.5

___________

-3.6 س = 16.2-

س = 4.5

عوض عن س في إحدى المعادلات 

2 ( 4.5 ) + ص = 7.5

ص = - 1.5 

الحل : ( 4.5 ، -1.5 )
                                        
 

¼ س + 4ص = ¾  2 

3س + ½ ص = ¼ 9 

 الجواب : 

اضرب المعالدة الاولى في 4 و المعادلة الثانية في 8 × 4 

 س+16 ص = 11 

96س + 16 ص = 296    اطرح المعادلتين 

_________ 

-95 س = -285 

 س= 3

عوض عن س في إحدى المعادلات 

ص == ½ 

 الحل : ( 3 ، ½ ) 

السؤال : هندسة: إذا علمت أن التمثيل البياني للمعادلتين س + ص = 6 ، 2س + ص = 9 يشتمل على ضلعين من أضلاع مثلث، وأن نقطة تقاطع المستقيمين هي رأس المثلث، فأجب عن الأسئلة الآتية:

أ- ما إحداثيات رأس المثلث ؟ 

ب- ارسم هذين المستقيمين وعين رأس المثلث ؟
ج- إذا كان التمثيل البياني للمعادلة س - ص = -3 يشمل الضلع الثالث للمثلث فأرسم هذا المستقيم على الشكل نفسه ؟

د- أوجد إحداثيات الرأسين الآخرين للمثلث ؟

الجواب : 

أ - رأس المثلث هي نقطة التقاطع أي حل المعادلتين 

س + 2 ص = 6       7س + 3 ص = -1 

2س + ص = 9   ×2      4س + 2ص = 18 

                            ________________

                        -3 س = -12 

                        س = 4

عوض عن س في إحدى المعادلات 

2 ( 4 ) + ص = 9

ص = 1

رأس المثلث ( 1.4 ) 

ب- س+ 2 ص= 6

عند س = 0   ص= 3 النقطة ( 0.3 ) 

ص = 0    س = 6 النقطة ( 0.6 ) 

2س +ص = 9

عند س = 0    ص = 9 النقطة ( 9.0 )

 ص = 0    س = 4.5 النقطة ( 0، 4.5 ) 

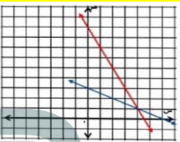
ج- س - ص = -3 

عند س = 0     ص = 3 النقطة ( 3.0 ) 

ص = 0   س= -3 النقطة ( 0.-3 ) 

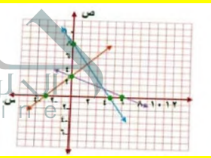
د- الرأسين الآخرين للمثلث ( 3.0 ) ( 5.2 ) 

السؤال : اختبارات: اكتشف معلم أنه عكس درجة أحد طلابه في اثناء رصدها مما أخر ترتيبه بين الأوائل، فأخبر الطالب وبين له أن مجموع رقمي درجته يساوي 14، والفارق بين درجتيه الحالية والصحيحة 36 درجة . وطلب إليه أن يعرف درجته الصحيحة وسوف يكافئه . فما الدرجة الصحيحة ؟
 

الجواب : درجته الصحيحة = 95 درجة

السؤال : تبرير: وضح كيف يمكنك تعرف نظام المعادلتين الخطيتين الذي له عدد لا نهائي من الحلول.

الجواب : عندما تكون إحدى المعادلتين مضاعفة للأخرى

السؤال : اكتشف الخطأ: حل كل من سعيد وحسين نظاماً من معادلتين، فأيهما إجابته صحيحة ؟ فسر إجابتك.

الجواب : سعيد لأنه حذف المتغير بضرب المعادلة الثنائية في 2 

ثم اطرح أما حسين فلم يطرح  المعادلتين بصورة صحيحة 

السؤال : مسألة مفتوحة: اكتب نظاماً من معادلتين يمكن حله بضرب إحدى معادلتيه في -3 ، ثم جمع المعادلتين معاً.

الجواب :

2س - ص  = 8  × -3       -6س + 3ص = -24

س - 3 ص = 9              س - 3 ص = 9

                              _______________

                              -5 س = -15 

                              س = 3

عوض عن س في إحدى المعادلات 

3-3 ص = 9

-3 ص = 6

ص = -2 

الحل ( 3، -2 ) 

السؤال : تحد إذا كان 4س + 5ص =2 ، 6س -2ص ب هو ( أ.3 ) فاوجد قيمة كل من : أب موضحا خطوات الحل التي استعملها ؟

الجواب :

التعويض عن س ، ص بالنقطة ( 3 ، أ ) 

4س + 5ص = 2 

12 + 5 أ = 2 

5أ = -10

أ = -2 

بالتعويض عن 6س - 2ص = ب 

18 - 2 × -2 = ب 

18 + 4 = ب 

السؤال : اكتب : وضح كيف تحدد المتغير الذي ينبغي حذفه باستعمال الضرب 

الجواب : 

حدد المتغير الذي  يكون إشارته مختلفة و يمكن أن يتساوى معاملة في المعادلتين في عدد معين بحيث يمكن حذفه بجمع المعادلتين

السؤال : ما الزوج المرتب الذي يمثل حل النظام الآتي؟

2س - 3ص = -9 

-س +3ص = 6 

أ- 3،3 

ب- -3.3

ج- 1،-3  ( صح ) 

د- 1، -3 

السؤال : احتمال: يبين الجدول أدناه نتائج رمي مكعب أرقام . فما الاحتمال التجريبي لظهور العدد 3؟

أ- ⅔ 

ب- ⅓ ( صح ) 

ج- 0.2 

د- 0.1

السؤال : حل كلا من أنظمة المعادلات الآتية مستعملاً طريقة الحذف:

6ق + هـ = -7 

6ق + 3 هـ = -9 

الجواب : 

6ق + هـ = -7 

6ق + 3 هـ = -9     اطرح المعادلتين

_______________

-2هـ = 2

هـ =-1 

عوض عن هـ في إحدى المعادلات 

6ق + 3 ( -1 ) = -9 

6ق = -6 

ق = -1 

الحل ( -1 ، -1 )

5س + 3ك = -9

3س +3ك = -3 

الجواب : 

5س + 3ك = -9

3س +3ك = -3   اطرح المعادلتين 

_____________

2س = -6 

س = -3 

عوض عن س في إحدى المعادلات 

3 ( -3 ) + 3 ك = -3 

3ك = 6 

ك = 2 

الحل : ( -3 ، 2 ) 

2س - 4ز = 6 

س - 4ز = -3 

الجواب : 

2س - 4ز = 6 

س - 4ز = -3    اجمع المعادلتين 

__________

س= 9 

عوض عن س في إحدى المعادلات 

2 ( 9 ) -4 ز = 6 

-4ز= -12

ز= 3 

 الحل : ( 9، 3 ) 

السؤال : حل كل متباينة فيما يأتي ، ومثل مجموعة حلها بيانياً:

 / م - 5 / < 8 

الجواب :

م - 5 < 8     أو  م - 5 > -8 

م < 13       أو م > -3 

مجموعة الحل : ( -3 < م < 13 ) 

/ ك +11 / < 5

الجواب : 

ك + 11 < 5  أو   ك +11 > -5 

ك < -6       أو   ك < -16 

مجموعة الحل : ( -6 > ك > -16 ) 

/ 2 و + 9 / > 11 

الجواب :

2 و + 9 > 11     أو 2 و + 9 < -11 

2و > 2        أو     2 و < -20

و > 1       أو  و < -10 

مجموعة الحل : ( و > 1 أو   و < -10 ) 

/2ر +1 / > 9

الجواب : 

2ر + 1 > 9     أو 2ر + 1 < -9

2ر > 8          أو 2 < -10 

ر > 4         أو ر < -5 

مجموعة الحل : ( ر > 4 أو ر < -5 ) 

السؤال : إذا علمت ان د ( س ) = 3 س -1 فما قيمة د ( -4 ) ؟ 

الجواب : 

د ( س ) = 3س -1 

د ( -4 ) = 3 ( -4 ) -1 

= -12 -1 = -13

استعد للدرس اللاحق

السؤال : اكتب الصيغة التي تعبر عن الجملة في كل مما يأتي:

أ- مساحة المثلث (م) تساوي نصف حاصل ضرب طول القاعدة (ل) في الارتفاع (ع).

الجواب : 

م = ½ ل ع 
 

ب- محيط الدائرة (مح) يساوي حاصل ضرب 2 في (ط) في نصف القطر (نق) .

الجواب : 

مح = 2ط نق 

ج- حجم المنشور القائم (ح) يساوي حاصل ضرب الطول (ل) في العرض (ع) في الأرتفاع (أ) .

الجواب : 

ح = ل ع أ