حل درس حل نظام من معادلتين خطيتين بالتعويض رياضيات ثالث متوسط
تحقق من فهمك
ص = 4س - 6
5س + 3ص = -1
الجواب :
الخطوة الاولى : إحدى المعادلتين مكتوبة اساسا بالنسبة لـ ص
الخطوة الثانية : عوض 4س - 6 بدلا من ص في المعادلة الثانية
5س + 3 ( 4 س - 6 ) = -1
5س +12 س - 18 = -1
17 س - 18 = -1
17 س = 17
س = 1
الخطوة الثالثة : عوض 1 بدلا من س في اي من المعادلتين لإيجاد قيمة ص
ص = 4 ( 1 ) -6 = -2
الحل هو ( 1 ، -2 )
2س + 5ص = -1
ص = 3س +10
الجواب :
الخطوة الاولى : إحدى المعادلتين مكتوبة اساسا بالنسبة لـ ص
الخطوة الثانية : عوض 3س + 10 بدلا من ص في المعادلة الثانية
2س + 5 ( 3س + 10 ) = -1
2س + 15 س + 50 = -1
17 س = -51
س = -3
الخطوة الثالثة : عوض -3 بدلا من س في اي من المعادلتين لإيجاد قيمة ص
ص = 3 ( -3 ) + 10 = 1
الحل هو ( -3 ، 1 )
4س + 5ص = 11
ص - 3س = -13
الجواب :
الخطوة الاولى : حل المعادلة الثانية بالنسبة للمتغير ص لان
معامل ص = 1 ، ص = 3س -13
الخطوة الثانية : عوض 3س - 13 بدلا من ص في المعادلة الثانية
4س + 5 ( 3س - 13 ) = 11
4س + 15 س - 65 = 11
19 س = 76
س= 4
الخطوة الثالثة : عوض 4 بدال من س في أي من المعادلتين لإيجاد قيمة ص
ص = 3 ( 4 ) - 13
ص = -1
الحل هو ( 4 ، -1 )
س - 3ص = -9
5س - 2س = 7
الجواب :
الخطوة الاولى : حل المعادلة الثانية بالنسبة للمتغير س لأن معامل س = 1 ، س = 3ص -9
الخطوة الثانية : عوض 3ص - 9 بدلا من س
5 ( 3ص - 9 ) -2ص = 7
15 ص - 45 -2ص = 7
ص = 4
الخطوة الثالثة : عوض عن ص = 4 في إحدى المعادلتين
س = 3 ( 4 ) -9
س = 3
الحل هو ( 3 ، 4 )
السؤال : حل كلا من النظامين الآتيين مستعملاً التعويض
2س -ص = 8
ص = 2س -3
الجواب :
عوض عن ص ب 2س - 3
2س - ( 2س -3 ) = 8
2س - 2س +3 = 8
2= 8
لا يوجد حل النظام
4س -3ص = 1
6ص - 8س = -2
الجواب :
حل المعادلة الاولى بالنسبة للمتغير س
س = ¾ ص + ¼
عوض عن س في المعادلة الثانية بـ ¾ ص +¼
6ص -8 ( ¾ ص + ¼ ) = -2
6ص -6 -2 = -2
-2 =-2
بما ان الجملة الناتجة تشكل متطابقة إذا يوجد عدد لا نهائي من الحلول
السؤال : رياضة: مجموع النقاط التي سجلها فريقان في إحدى مباريات كرة اليد 31 نقطة. فإذا كان عدد نقاط الفريق الأول يساوي 5,2 أمثال عدد نقاط الفريق الثاني، فما عدد نقاط كل فريق؟
الجواب :
نفترض ان عدد نقاط الفريق الاول س ، عدد نقاط الر=فريق الثاني ص
س + ص = 31
ص= 31- س
س = 5.2 ص
عوض عن ص في النعادلة الثانية بـ 31 -س
س= 5.2 ( 31 - س )
س = 161.2 - 5.2 س
6.2 س = 161.2
س = 26
ص = 31 -26
ص = 5
عدد نقاط الفريق الاول 26 و عددنقاط الفريق الثاني 5
تأكد
السؤال: حل كلا من الأنظمة الآتية مستعملا التعويض
س = ص - 2
4س + ص = 2
الجواب :
بما ان المعادلة الاولى محلولة بالنسبة لـ س
عوض في المعادلة الثانية عن س = ص - 2
4 ( ص -2 ) + ص = 2
4ص - 8 + ص = 2
5ص = 10
ص = 2 عوض في المعادلة الاولى عن ص = 2
س = 2-2 = 0 فالحل ( 2.0 )
2س + 3ص = 4
4س +6ص = 9
الجواب :
حلا المعادلة الاولى بالنسبة ل ص
2س - 2س +3ص = 4-2 س
3ص = 4 -2 س
ص = 4/3 -⅔ س
عوض عن ص في المعادلة الثانية :
4س + 6 ( 4/3 -⅔ س ) = 9
4س +8-4س = 9
8 = 9
النظام لا يوجد له حل
س - ص = 1
3س -3ص +3
الجواب :
حل المعادلة الاولى بالنسبة لـ س
س = ص + 1
عوض في المعادلة الثانية عن س
3 ( ص + 1 ) = 3ص +3
3ص +3 = 3ص +3
بما ان طرفي المعادلة يمثلان متطابقة إذا له عدد لا نهائي من الحلول
السؤال :هندسة : إذا كان مجموع قياسي الزاويتين س، ص يساوي 180، وقياس الزاوية س يزيد بمقدار 24 على قياس الزاوية ص، فأجب عما يأتي :
أ- اكتب نظاما من معادلتين لتمثيل هذا الموقف
ب- اوجد قياس كل زاوية
الجواب :
أ- معادلتي النظام : س + ص = 180
س = ص +24
بما ان المعادلة الثانية محلولة بالنسبة لـ س
عوض في المعادلة الاولى عن س = ص +24
ص +24 + ص = 180
2ص +24 = 180
2ص = 156
بالتعويض في المعادلة الثانية
س = 78 +24 = 102
السؤال : حل كلا من الأنظمة الآتية مستعملاً التعويض:
ص = 4س + 5
2س + ص = 17
الجواب :
بما ان المعادلة الثانية محلولة بالنسبة لـ ص
عوض في المعادلة الثانية عن ص = 4س +5
2س +4س +5 =17
6س +5 =17
6س =12
س =2
بالتعويض في المعادلة الثانية س = 2
ص = 4 ( 2 ) + 5 = 13
الحل هو : ( 2، 13 )
ص = 3س -34
ص = 2س -5
الجواب :
عوض عن ص في إحدى المعادلتين
3س - 34 = 2س -5
3س -2س =34 -5
س = 29
عوض عن س في إحدى المعادلتين
ص = 3 ( 29 ) -34
ص = 53
الحل: ( 29 ، 53 )
ص = 3س - 2
ص = 2س -5
الجواب :
عوض عن ص في إحدى المعادلتين
3س - 2س = 2-5
3س -2س = 34 -5
س = -3
عوض عن س في إحدى المعادلتين
ص = 3 ( -3 ) -2 = -11
الحل : ( -3 ، -11 )
2س + ص = 3
4س + 4ص = 8
الجواب :
حل المعادلة الاولى بالنسبة لـ ص
ص = -2 س +3
عوض في المعادلة الثانية عن ص = -2س +3
4س +4 ( -2س +3 ) = 8
4س - 8س +12 = 8
-4س +12 =8
-4س = -4
س = 1
عوض عن س = 1 في المعادلة الثانية
4 ( 1 ) +4ص = 8
4+4ص = 8
4س = 4
ص = 1
الحل : ( 1 ، 1 )
3س +4ص = -3
س +2ص = -1
الجواب :
بما ان المعادلة الثانية محلولة بالنسبة لـ س
س = -2ص -1
عوض في المعادلة الاولى عن س = -2 ص -1
3 ( -2 ص -1 ) +4ص = -3
-6ص -3+4ص = -3
-2 ص = 0
ص = 0
بالتعويض في المعادلة الثانية ص = 0
س = -1
الحل هو ( -1 ، 0 )
-1 = 2س - ص
8س - 4ص = -4
الجواب :
حل المعادلة الاولى بالنسبة لـ ص
ص = 2س +1 ط عوض عن ص في المعادلة الثانية
8س - 4 ( 2س +1 ) = -4
8س - 8س - 4 = -4
-4 = -4
بما ان طرفي المعادلة تمثل متطابقة فلها عدد لا نهائي من الحلول
س = ص - 1
-س + ص= -1
الجواب :
عوض عن س في المعادلة الثانية
( ص - 1 ) + ص = -1
-ص + 1 +ص = -1
+1 = -1
لا يوجد حل للنظام
ص = -4س + 11
3س +ص = 9
الجواب :
حل المعادلة الثانية بالنسبة لـ ص
ص = -3 س +9
عوض عن ص في المعادلة الاولى
-3س +9 = -4س +11
4س -3س = 11 -9
س = 2
عوض عن س = 2 في المعادلة الثانية
3 ( 2 ) + ص = 9
6 +ص = 9
ص = 3
الحل ( 2، 3 )
ص = -3س +1
2س + ص = 1
الجواب :
حل المعادلة الثانية بالنسبة لـ ص
ص = -2س +1
عوض عن ص في المعادلة الاولى
-2س + 1 = -3س +1
3س -2س = 1-1
س = 0
المعادلة الثانية
2 ( 0 ) + ص = 1
ص = 1
الحل هو : ( 1،0 )
3س + ص = -5
6س + 2س = 10
الجواب :
حل المعادلة الاولى بالنسبة لـ ص
ص = -3س -5
عوض عن ص في المعادلة الثانية
6س + 2 ( -3س -5 ) = 10
6س -6س -10 = 10
-10 = 10
لا يوجد حل للنظام
5س - ص = 5
-س +3ص = 13
الجواب :
حل المعادلة الاولى بالنسبة لـ ص
ص = 5س -5
عوض في المعادلة الثانية عن ص = 5س -5
-س +3 ( 5س -5 ) = 13
-س +15 س - 15 = 13
14س = 28
س = 2
بالتعويض في المعادلة الثانية س = 2
5 ( 2 ) - ص = 5
10 -ص = 5
ص = 5
الحل هو : ( 2 ، 5 )
-5 س + 4ص = 20
10س - 8ص = -40
الجواب :
حل المعادلة الثانية بالنسبة لـ ص
8ص = 10س +40
ص = 5/4 س + 5
عوض في المعادلة الثانية
10س - 8 = -40
10س - 10س - 40 = -40
-40 = -40
طرفي المعادلة يمثلان متطابقة النظام له عدد لا نهائي من الحلول
السؤال : سياحة: يبين الجدول أدناه العدد التقريبي لزوار منطقتين سياحيتين في المملكة خلال عام 1425هـ، ومعدل التغير بالآلاف خلال السنة الواحدة:
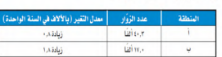
أ- عرف المتغيرات و اكتب معادلة تمثل عدد زوار كل منطقة
ب- إذا استمرت الزيادة بالمعدل نفسه فبعد كم سنة تتوقع ان يصبح عدد الزوار متساويا في المنطقتين ؟
الجواب :
أ- س هي عدد زوار المنكقة ، ص هي عدد السنوات
س = 40.3 + 0.8 ص
س = 17 +1.8 ص
ب- 40.3 +0.8 ص = 17 +1.8 ص
1.8 ص - 0.8 ص = 40.3 -17
ص = 23.3 اي بعد 23 سنة و 3 أشهر
السؤال : رياضة: يبين الجدول المجاور الزمن المسجلللاعبين في سباقات الماراثون خلال عامي 1425هـ ، 1430هـ .
| العام | اللاعب أ | اللاعب ب |
| 1425 هـ | 1:51:39 | 1:54:43 |
| 1430 هـ | 1:49:31 | 1:58:03 |
أ- إذا سجل الزمن لكل منهما بالساعات و الدقائق و الثواني فأعد كتابته إلى أقرب دقيقة
| العام | اللاعب أ | اللاعب ب |
| 1425 | 112 | 115 |
| 1430 | 110 | 118 |
ب- إذا اعتبرنا العام 1425 هـ صفرا و افترضا ثبات معدل التغير بعد عام 1425 هـ فاكتب معادلة تمثل الزمن المسجل ( ص ) لكلا اللاعبين في أي عام ( س )
الجواب :
ص = -0.4 س + 112
ص = 0.6 س +115
جـ - إذا استمر النغير في الاتجاه نفسه فهل يسجلان الزمن نفسه ؟ فسر إجابتك ؟
الجواب :
لا لأن التمثيلين لا يتقاطعان
السؤال : تحد: كان عدد المتطوعين في العمل الخيري في إحدى القرى 60 متطوعاً، فإذا كانت نسبة الرجال إلى النساء 7 : 5 ، فأوجد عدد كل من الرجال والنساء المتطوعين.
الجواب :
س + ص = 660
7س = 5ص
س = 60 -ص
7 ( 60 -ص ) = 5ص
420 - 7ص = 5ص
12 ص = 420
ص = 35
س = 60 - 35
س = 25
عدد النساء 25 عدد الرجال = 35
السؤال : تبرير: قارن بين حل نظام من معادلتين بكل من : طريقة التمثيل البياني، وطريقة التعويض.
الجواب :
حل نظام معادلتيين بطريقة التمثيل البياني يستدعي التعويض في المعادلات بنقتط مختلفة للوصول إلى الرسم البياني المناسب و نوحد الحل من الرسم حيث تكون نقطة التقاطع
أما حل نظام معادلتين بطريقة التعويض نوجد قيمة أحد المتغيرين بالنسبة للمتغير الآخر ثم نعوض به في المعادلة لتكون معادلة من متغير واحد يمكن حلها جبيا ثم نعوض بالقيمة في إحدى المعادلتين لإيجاد قيمة المتغير الآخر
السؤال : مسألة مفتوحة: أنشىء نظاماً من معادلتين له حل واحد، ووضح كيف يمكن أن يعبر عن مسألة من واقع الحياة، وصف دلالته.
الجواب :
المعادلتين 2س - ص = 3 5ص - 3س = 6
يعبر النظام عن معدل إنتاج مصنع خلال سنوات منذ بداية عمله
حيث س هي عدد سنوات عمل المصنع و ص هي معدل الإنتاج
السؤال : اكتب وضح كيف تحدد الأفضل تعويضا عند استعمال طريقة التعويض لحل نظام من معادلتين
الجواب :
الأفضل تعويضا هو المتغسر الذي يكون معامله يساوي 1
تحل المعادلة بالنسبة له ثم يعوض عنه في المعادلة الاخرى
السؤال : أي الأنظمة الآتية له حل واحد؟
أ- ص = -3س + 4
-6 س -2ص = -8
ب- ص = 5س +1
4س +ص = 10 ( صح )
جـ - س + ص = 1
س = 3-س
السؤال : ما مجموعة حل المعادلة : 2/ ف / = 16 إذا كان ف عددا صحيحا ؟
أ- 8،0
ب- 0.8-
جـ- : -8 ، 8 ( صح )
د- -8 ، 0 ، 8
السؤال : مثل كلا من أنظمة المعادلات الآتية بيانياً، ثم حدد ما إذا كان له حل واحد أم عدد لا نهائي من الحلول أم ليس له حل، وإن كان له حل واحد فاكتبه.
س = 1
2س -ص = 7
الجواب :
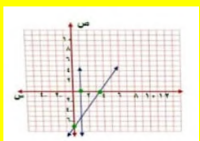
بما ان س = 1 يتم رسم مستقيم يوازي محور الصادات
عند س = 0 ص = -7 النقطة ( 0 ، -7 )
ص = 0 س = 3.5 النقطة ( 3.5 ، 0 )
للنظام حل واحد هو نقطة التقاطع ( 1 ، 5- )
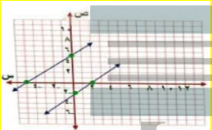
ص = س + 5
ص = س -2
الجواب :
ص = س + 5
عند س = 0 ص = 5 النقطة ( 5،0 )
ص = 0 س = -5 النقطة ( 0.-5 )
ص = س -2
عند س = 0 ص = -2 النقطة ( 0 ، -2 )
ص = 0 س = 2 النقطة ( 0،2 )
بما أن المستقيمان متوازيان فالنظام ليس له حل
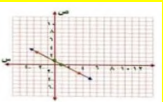
س + ص = 1
3ص + 3س = 3
الجواب :
س + ص = 1
عند س = 0 ص = 1 النقطة ( 1،0 )
ص = 0 س = 1 النقطة ( 0،1 )
3ص + 3س = 3
عند س = 0 ص = 1 النقطة ( 1،0 )
ص = 0 س = 1 النقطة (0،1 )
بما ان المستقيمان منطبقان فالنظام له عدد لا نهائي من الحلول
السؤال : حل كل متباينة فيما يأتي ، وتحقق من صحة الحل:
6ف + 1 > -11
الجواب :
6ف + 1 - 1 > -11 -1
6ف > -12
ف > -2
مجموعة الحل ( ف > -2 )
24 > 18 + 2 ن
الجواب :
24 -18 > 18 -18 +2 ن
6> 2ن
3 > ن
مجموعة الحل ( ن < 3 )
-11 > 2/5 ف + 5
الجواب :
-55 > 2 ف + 25
-55 -25 > 2 ف + 25 - جو 25
-80 > 2
- > 40 ف
مجموعة الحل : ( ف < -40 )
السؤال : اكتب معادلة المستقيم المار بالنقطتين ( 1،6 ) ، ( 1 ، 1 )
الجواب :
ص 2 / م-2
م = 1-1 /6-1 = -0/5 = 0
ص = م س + ب
1 = ب
المعادلة هي ص = 1
استعد للدرس اللاحق
السؤال :بسط كلا من العبارات التالية بعد استعمال خاصية التوزيع
10 ب + 5 ( 3 + 9 ب )
الجواب :
10ب + 15 + 45 ب
55ب +15
5 ( 11 ب + 3 )
5 ( 3ن ^2 + 4 ) - 8ن
الجواب :
15ن ^2 + 20 -8 ن
15 ن ^2 + 20
-2 ( 7 أ + 5 ب ) + 5 ( 2 أ -7 ب )
الجواب :
-14 أ - 10 ب +10 أ - 35 ب
( -14 +10 أ ) + ( 10 ب - 35 ب )
-4 أ - 25 ب



